[88] The Hot-Hand Artifact for Dummies & Behavioral Scientists

A friend recently asked for my take on the Miller and Sanjurjo's (2018; pdf) debunking of the hot hand fallacy. In that paper, the authors provide a brilliant and surprising observation missed by hundreds of people who had thought about the issue before, including the classic Gilovich, Vallone, & Tverksy (1985 .htm).

In this post:
(1) I try to provide an intuitive explanation for the Miller & Sanjurjo critique, and
(2) explain why I still believe in the hot hand fallacy [1].

Definitions: hot hand, and hot hand fallacy
Hot hand: players are more likely to make a shot after making some shots. Say, after three :
                     hot hand:                  P(H|HHH)> P(H)
                              notation: P(H|HHH) is read as "probability of making the next shot:  P(H, after 3 shots are made  |HHH)".

Hot hand fallacy: people believe the hot hand is bigger than it is : 
                      hot hand fallacy:      P̂(H|HHH) > P(H|HHH)
                                notation: P̂( H|HHH) is read as "predicted probability of making the next shot:  P̂(H, after 3 shots are made  |HHH)".

Importantly, both can coexist. For example, Steph Curry might convert 45% of his three-point shots in general, increasing to 50% after making two in a row, but people believe it increases to 60%.

Claims about sports vs about thinking
Gilovich et al 1985 made two central claims: (1) the hot hand is basically zero, and (2) people over-perceive hot hands. Miller and Sanjurjo found evidence consistent with the hot hand in Gilovich et al's data, contradicting claim (1); it is not wrong to believe in the hot hand to some degree. I am hopeful (as are they) that their findings will refocus the field's attention to claim (2) which I find more important for behavioral science.  This quote from Matthew Rabin (2002; .pdf), describing the phenomenon with the more accurate label "hot hand bias", captures the perspective I hope we will all move towards (p.805): 

Gilovich, Vallone, and Tversky [1985] […] demonstrated that, while basketball fans believe that basketball players are streak shooters […] such a hot hand does not in fact exist (or at least not nearly to the degree that people believe in it).  

To be clear, Miller & Sanjurjo's discovery must be taken into account also when studying the second claim. I do so here. 

Hot hand artifact
To determine if there is a hot hand, we must compare the players’ likelihood to make a shot after a streak, P(H|streak), to some benchmark. The benchmark that researchers have used is the overall probability of making a shot: P(H). This assumes that, in the absence of a “hot hand”, we should see P(H|Streak)=P(H).  Miller and Sanjurjo discovered that this is incorrect given the way researchers have defined “streak”. This leads researchers to under-detect true hot hands, and therefore to overestimate the magnitude of the hot-hand fallacy. I refer to this issue as the 'hot hand artifact' [2].

To understand the hot hand artifact, we need to differentiate between streaks and substreaks:

Streaks are sets of consecutive hits, starting with the first hit in the set.
Substreaks are subsets of streaks, starting with any hit in the streak.

A streak of 2 means there have been 2 hits in a row.
A substreak of 2 means there have been at least 2 hits in a row.

If you flip a coin 3 times and get Heads three times:

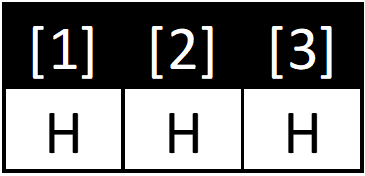
• There is only one streak of HH:         [1][2]
• There are two substreaks of HH:       [1][2] & [2][3]

I next simply state the hot hand artifact, I explain it afterwards.

Stating the hot hand artifact
The hot hand artifact arises when researchers compute how likely a hit is after substreaks rather than streaks of hits.

Let's do coins. If you look for streaks, heads is always 50%:
P(H|HHH)=P(H|HH)=P(H|H)=P(H)=.5

But if you look at substreaks, that's not true.
After a substreak of HH, the probability of another H is <50%.
That’s extremely nonintuitive, so let's go over it in baby-steps.

Let's represent a substreak by putting a '__' before the Hs; thus a substreak of 3 is _HHH.
Then, we have this definition of the hot hand artifact, with say 3 hits:

            hot hand artifact: P(H|_HHH) < P(H)

So to recap:
            hot hand:             P(H|HHH) > P(H)
            hot hand fallacy:  P̂(H|HHH) > P(H|HHH)
            hot hand artifact: P(H|_HHH) < P(H)

Initial intuition for why substreaks matter: Why P(H|_H)<P(H)?
Imagine a weird coin that always comes up Heads 10 times in a row, then 1 Tails, then 10 Heads, then 1 Tails, etc.

HHHHHHHHHHTHHHHHHHHHHTHHHHHHHHHHT…

How likely is H, after 9 H in a row (i.e., P(H|HHHHHHHHH)?
Depends on whether we mean a streak of (exactly) 9 or a substreak of (at least) 9.

If we mean a streak of 9, the answer is "100%"; this weird coin always gets 10 H in a row.
If we mean a substreak of 9, the answer is… …50%.

When the substreak starts with the 1^st H, it is 100%
When the substreak starts with the 2^nd H, it is 0%
On average, 50%.

Second baby step: a normal coin
I now reproduce the 1^st example in Miller & Sanjurjo 2018, doing the hot hand artifact calculations for a 50:50 coin tossed three times. I explain it a bit differently, but it is the same example (see their Table 1 .png).

 

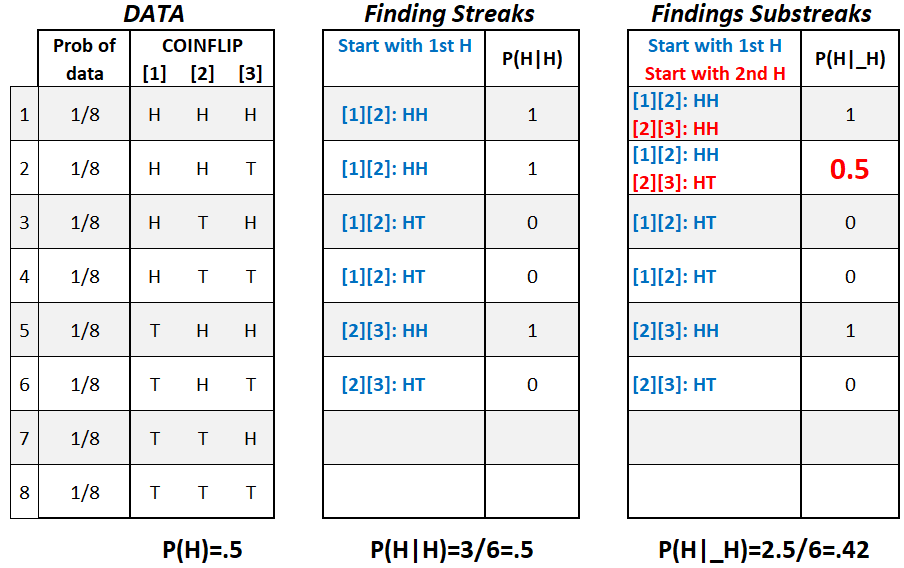
Tossing 3 coins there are 2³=8 possible outcomes.
Streaks:        After flipping exactly 1 Heads, 50% of the time we see Heads again.
Substreaks:  After flipping at least 1 Heads, 42% of the time we see Heads again.

The only difficult thing here is that 2^nd row: HHT.
If you understand that row, you understand the hot hand artifact.
So let's focus on that row.

In the middle table: starting with the first H, we can only get HH
In the right table: starting with the first H, we also get HH, but starting with the 2^nd H, we get HT: so P(H|_H)=.5. By expanding our search to substreaks, this second row lowers the share of HH from 100% to 50%. When we average this now lower row with the others, we obtain P(H|_H)<P(H).

Here is another way of thinking about it. There are two stages. First, data are generated. There is no bias there, coin is unbiased. Second, we search the data for substreaks, and our search is biased. If we find an HT we stop the search, if we find HH we keep looking, thus giving HT more chances.

How the hot hand artifact challenges the evidence of the hot hand fallacy
Having understood streaks vs substreaks, and why P(H|_H)<P(H) let's see why this matters for hot hand research.

Recall that:
hot hand fallacy: P̂(H|HHH) > P(H|HHH)

To study the hot hand fallacy, then, we need to compare P̂() and P(),perceived and real hand-hotness.

We estimate the former from participants, asking: "when a player makes 3 in a row, how likely are they to make a 4^th?". We estimate the latter from 'real' data (e.g., NBA data), and it is in the real data that the hot hand artifact matters. This is because researchers have looked for substreaks rather than streaks.

Researchers looked at how often players hit a shot after 3 in a row, without restricting the search to having made only 3 in a row. Looking at substreaks of shots has led researchers to under-estimate real hand-hotness. This is simply a brilliant insight by Miller and Sanjurjo.

Thus, the criticism is that hot hand fallacy researchers found this:
P̂(H|HHH)          >              P(H|_HHH)

But it could be that:
P̂(H|HHH) = P(H|HHH) > P(H|_HHH)

In words, it is possible that rather than people over-estimating hot hands, researchers under-estimated them.

For instance, Gilovich et al in one study estimate the true hot hand to be +3%, p = .49 (comparing shooting % after making vs missing 3 shots).  Miller & Sanjurjo correct for the hot hand artifact and put the estimate at 13% (with a wide CI: approx 4%-22%) [3].

Why I still believe in the hot hand fallacy
I still believe in the hot hand fallacy for many reasons: First, it follows naturally from lots of things we have learned since 1985, see e.g., the review by Alter & Oppenheimer (2006; .pdf). Second, I look around. People everywhere interpret 'trends' after seeing just two datapoints (in sports, politics, faculty meetings, etc.). Third, and most relevant, I still believe in the hot hand fallacy, because it is present in the classic 1985 hot hand paper even taking into account the hot hand artifact. I will discuss two findings.

Finding 1. Two free-throws
Gilovich et al. report that participants expected an NBA player with a 70% free-throw average to make 74% of shots after making one, and 66% after missing one. An 8% difference in the estimate of P̂(H|H) – P̂(H|M).

Gilovich et al contrasted that 8% in perceived streakiness, with their estimated actual streakiness of NBA free-throws: 0% [4]  Because free-throws were analyzed in sets of two, there are no substreaks, no hot hand artifact.

Miller & Sanjurjo discussed these data in their footnote 22, which I have transcribed, and commented on, in this footnote [5]

Finding  2. 100 single-shot predictions.
Another result by Gilovich et al which is not threatened by the hot hand artifact is Study 4, where 26 varsity players took 100 shots each, predicting each time if they would make the next shot (putting money on the line). While here we do look at substreaks, a previous hit may have been preceded by other hits, we are contrasting shots after substreaks with predictions after the same substreak, so the hot hand artifact cancels out.

Players were much more likely to bet that they would make a shot after making rather than missing  the previous shot.  But they were wrong. Previous shots did not predict future shots. Overall, the correlation between making the previous shot and predicting making the next shot was r=.4, while the correlation between making the previous shot and actually making the next was just r=.05.

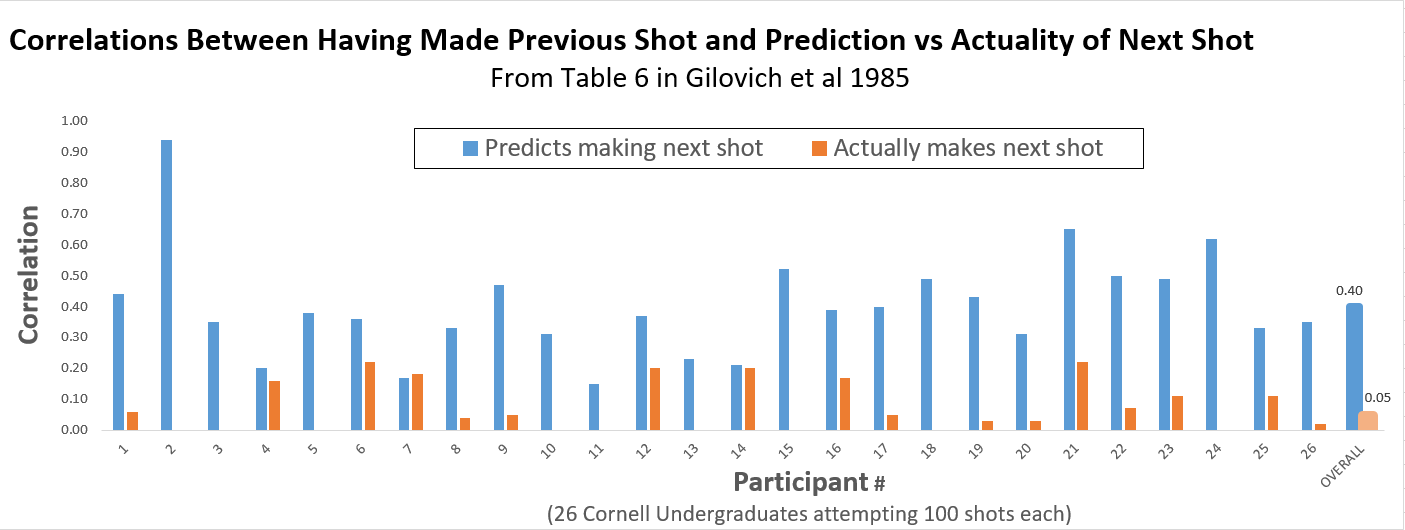
   Predicted impact of previous shot:  r=.40
–  Actual impact of previous shot        r=.05
= hot hand fallacy.

This finding was replicated in a sample of Israeli Olympiads, obtaining r=.45 & r=.06 respectively  (Avugos et al., 2013 .pdf) [6]

My favorite fact for this post: calibration of massiveness of hot hand fallacy
It is worth noting that expecting r=.40 for consecutive shots (see chart above) implies implausibly strong hand-hotness. As a calibration, I simulated a player that when cold (previous shot was missed) makes as few shots as the NBA player with the lowest shooting percentage in the 2019-2020 season (Taurean Prince: 37.6%), but then gets dramatically better with each basket that he makes until, after three consecutive hits, he acquires the best shooting percentage in the league, 74.2%, that of Mitchell Robinson. In a series of 100 shots, this impossibly hot-handed player would on average have a correlation of r=.17 for two consecutive shots (R Code).

In the Gilovich et al study, and in the Israeli replication, people expected their hand-hotness to be more than twice this implausible upper bound. [7].

I am using what participants predicted ("hit" vs "miss") as a proxy for the probability they assigned a hit or a miss. This is more of a leap of faith than seems at first, but I think a reasonable one. See footnote for details [8]  

Conclusions
The hot hand artifact discovered by Miller and Sanjurjo is extraordinarily nonintuitive and it was pursued in an extremely clever, thorough, and elegant manner. But, when we focus on the evidence supporting the hot hand fallacy, the psychologically interesting, and practically consequential finding that people misinterpret meaningless random noise as meaningful streaks that they fallaciously expect to persist, that evidence is not challenged by the hot hand artifact. 

---

---

Footnotes.

1. In conversations with Adam Sanjuarjo he persuaded me the term hot hand bias, which they used in earlier versions of the paper, would be more accurate than fallacy, but he also persuaded people would confuse 'hot hand bias' with the selection bias they discovered; so I ended up sticking with fallacy. [↩]
2. Miller & Sanjurjo refer to it as the streak selection bias, but given the definition of 'streak' I use in this post, such name would be confusing. [↩]
3. I obtained an approximate confidence interval for the 13% estimate by resampling under the null, obtaining a width of ~18%, which I apply symmetrically around the estimate of 13%, so 13+-9.   R Code [↩]
4. That 0% estimate came from just 9 players; but since then, it has been estimated to be in the 0-2% range using data from the entire league in a few different papers, 2% is much less than the perceived 8%. See next footnote for details. [↩]
5. Footnote 22 by Miller and Sanjurjo on Finding 1: illusory hot hand in free-throws.
   I paste here their footnote 22 followed by my take on it. By GVT they mean the original hot hand fallacy paper by Gilovich, Vallone & Tversky 1985

   I tend to agree with (i) and (ii), but my interpretation is different. The fact that we should not rationally expect one free throw to predict the next, means that free-throws are indeed not an ideal test of the sports question of whether there is a hot hand in basketball, but for that same reason they are a good test of the psychology question of whether there is a hot hand fallacy.  Even in a setting where streakiness should not be expected, people expect it. It's a conservative test, and the hot hand fallacy passes it with some comfort. In terms of (iii), I would add some nuance to the characterization that "subsequent studies … find evidence that is inconsistent with the conclusions that GVT give" (bold added). Specifically, the subsequent studies do challenge the claim that there is no hot hand at all, but support the claim that people over-perceive it:

   1. Goldman & Rao (2012): I did not find a result in the paper that spoke to P(H|H) vs P(H|M).
   2. Aharoni and Sarig (2011) write "As in GVT, we find no simple dependency between the outcomes of first and second FTs." (p.2311).
   3. Arkes 2010 (this Arkes is not Hal Arkes), finds about <3% hot hand.
   4. Miller & Sanjurjo (2014), same authors, previous paper, write "we find that the performance after a hit is not significantly better than after a miss in six out of seven seasons, with a difference of one percentage point or less in most seasons (though the difference is significant when all seasons are pooled together). P10.
   5. Yaari Eisenman (2011) finds an effect in the 2% range
   6. Wardrop (1995) "the hot hand phenomenon is not supported by these free throw data" (page 27)

   So my take of the follow-up work is that, with much larger samples than those used by Gilovich et al., the hot hand effect in free throws is in the 0-2% range, but people believe it is at about 4 times larger. Because 8%>2%, there is a hot hand fallacy.

   [↩]

6. Avugos et al report a second replication with recreational players, finding r=.249 and r=.002 for one variation, and r=.289 & r=.044 for the other. [↩]
7. Miller and Sanjurjo have a working paper looking at this study in GVT. In a nutshell they argue, correctly in my view, that the analyses are underpowered to detect true hand-hotness.  The calibration provided above is indeed consistent with that. But, I would add, the analyses are even more underpowered to detect people's perception of their own hand hotness. If people had calibrated beliefs about sequential dependency of their shots we should not be able to detect any sequential dependency in their predictions; but we do, big time. This goes back to the research question. These data are useful to study the psychological question of the hot hand fallacy, and not useful to study the sports question of the hot hand. [↩]

8. On making inferences about beliefs from observed  predictions .
   It is somewhat tricky to infer what participants believe from what they predict. Imagine someone who always predicts 'hit' if the expected probability is p>.5, and always predicts 'miss' otherwise. If the baseline is at P̂(H)=50%, then a tiny change in beliefs following a hit, say, going from 49.9% to 50.1%, could have a big effect in what participants predict. Adam Sanjurjo and Josh Miller brought this valid concern up in our conversations. There are three reasons I am not super concerned about over-interpreting this result (correlation of .40  vs .05 in Study 4). First, in practice, people don't make predictions in that bang-bang way. People don't predict 100% of hits, when they think the probability is 50.1%; rather, people 'probability match' (e.g., see  review by Vulkan 2000; htm). That is, when people think something has an x% chance of happening, they predict it x% of the time. Therefore, in practice, the more often people predict something the higher they perceive its probability to be. Second, if people did make bang-bang  predictions, attenuation, rather than exaggeration of measured hot hand fallacy seems likely. Unless all participants perceive the probability to be extremely close to 50% (or whatever cutoff people used for always saying "hit"or "miss"), then even large changes in beliefs do not change what people predict. e.g., if upon seeing someone score, the perceived probability of them scoring again goes from 35% to 45%, the prediction of "miss" is not changed. Third, in the Cornell data, there is some variation across players in their hit rate, ranging from making 25% to 61% of their shots across the 26 players. Yet we see a very strong correlations for previous shot made and next prediction for all of them, even those who are far from 50%. Moreover, there is no apparent association between distance from the 50% average and strength of the correlation between past shot and prediction for next shot:
   

   Thus while the inference rests on the assumption that people predict 'hit' more often if they think a 'hit' is more likely, the assumption seems reasonable. [↩]