There is a classic statistical test known as the Kolmogorov-Smirnov (KS) test (Wikipedia).
This post is about an off-label use of the KS-test that I don’t think people know about (not even Kolmogorov or Smirnov), and which seems useful for experimentalists in behavioral science and beyond (most useful, I think, for clinical trials and field experiments of policies that could backfire on some people).
If I’m wrong and the off-label use is known, well, that’s a little embarrassing, but please let me know.
Like the t-test, the KS-test can be used to compare two samples1The KS-test can also be used to compare one sample to a theoretical distribution, e.g., to assess if a sample is statistically significantly not-normally distributed. We relied on it to when assessing whether the Ariely insurance driving data were uniformly distributed, see footnote 5 in Colada[98] .
While the t-test involves only differences of means, the KS-test considers any type of difference across samples. So, like the t-test, the KS-test could be statistically significant because the sample means are quite different, but, unlike the t-test, the KS-test could also be statistically significant because the sample variances are quite different, or the share of observations that are exactly 0 are quite different, etc.
The KS test is seldom used, but when it is used, it is used as a a test, as a way to obtain a p-value quantifying whether things are significantly different across groups2Or one group, see Footnote 1.
But, there is an off-label use of the KS-test, one that does not use it as a test, but as a way to estimate something. Specifically, it can estimate the share of observations in a between-subjects design that are impacted by the manipulation. So, instead of asking “Is the average of the dependent variable higher in A than in B?”, we can ask “How many people have a higher dependent variable in A than in B”? Again. This is noteworthy because it involves between subjects design where people are only in A or only in B so we don't know if any given individual has a higher DV in A or in B 3Technically, the KS test does not estimate the share showing an effect, it bounds it, meaning it tells you its smallest possible value, rather than its expected value. More on this later..
What does the KS-test do?
The KS test compares the entire distribution of values between samples (the CDFs). It quantifies the biggest observed difference in those distributions. Let's illustrate with data from an old paper of mine (.pdf) in which participants provided their valuation, in a between subject design, for either a $50 Gift Certificate, or for a 50:50 gamble that for sure paid either that $50 certificate, or a $100 one (people, puzzlingly, pay less for the lottery, the objectively superior alternative; this is known as the “Uncertainty Effect”.htm). The figure below has the CDFs. For example, if we were to draw a horizontal line (that unfortunately STATA didn't draw) at the 50th percentile, the medians are about $10 and $35. About half the people pay $10 or less for the lottery, and about half the people pay $35 or less for the $50 gift certificate.
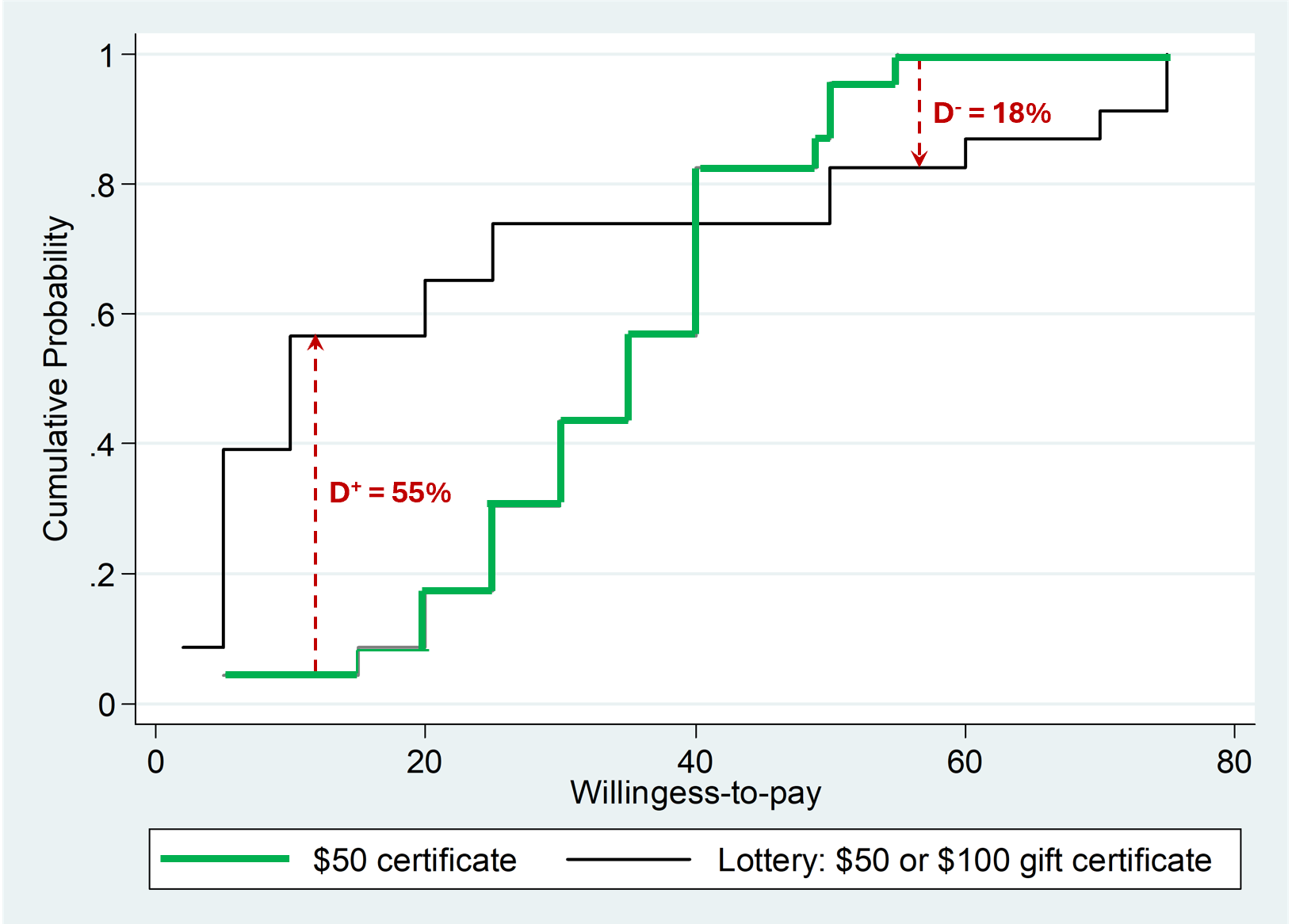
Fig 1. Distribution of valuations an the D+ and D- in a KS-test.
OK, let's now get to the KS test. It computes the biggest positive and negative differences in these CDFs. The biggest positive difference is about 55%, seen around $10. In the KS-test that's the D+ (test) statistic, the biggest positive difference. There is also the D–, flagged here with the 2nd arrow; D– = 18%.
Researchers and statisticians usually ignore those D+ and D- values, they usually do not even report them. But it is those D+ and D- that give us the off-label use. Those D values inform the share of people showing each effect. Returning to Figure 1 above, the Ds mean that at least 55% of participants pay more for the $50 gift certificate than for the lottery, and at least 18% of participants do the opposite.
The KS-test off-label use involves using D+ and D- as bounds on the share of people impacted positively vs negatively by treatment.
I should say I did not discover or prove this fact; a paper published in Econometric Theory in 2010 did. But the authors do not seem to have realized that that's what they proved (they do not mention the KS test in their paper). I wrote my personal journey to acquiring this tidbit of information, but it is long, so I put it behind the green button.
An intuition for this off-label use
The intuition behind the D+ and D- being bounds is actually straightforward, and in my nerdy opinion, intellectually stimulating. Let’s do an example. If we start with a binary dependent variable things are easier.
Let’s say we are studying whether people pay more for red or white wine. We run a study where people are offered either a red wine or a white wine, and are asked: “Would you pay $24 for this bottle?”
Imagine the share of ‘yesses’ is 72% for red and 42% for white.
How many people pay more for red than for white? Well, we don’t know, because for any person we only see their answer for either red or white. But we can bound it.
The only fact to keep in mind is that we estimate a 30% change in the share of people who are willing to pay $24. It's useful to spell out what that 30% of people entails. Those are people that would pay less than $24 for white wine, but would pay more than $24 for red wine. For example someone who would pay $10 for white and $30 for red is there.
It’s possible that 100% of people pay more for red wine in general, but only 30% are in the sweetspot that crosses over $24. For example, if Marjorie pays $10 for White and $20 for red, she shows an effect, but not in our sample, as she would not buy either wine. If Marco pays $26 for White and $30 for red, same idea: exhibits an effect which we do not observe. Because some people exhibit an effect that's not observable, it's possible that 100% of people exhibit the effect.
It’s similarly possible that 75% of people exhibit an effect but we observe only 30%.
It’s similarly possible that 50% of people exhibit an effect but we observe only 30%.
Many things are possible, but usefully, some are impossible6For ease of exposition I use the term possible/impossible, but this is ignoring sampling error, so the statements are probabilistic, requiring statistical inference. One way of thinking about it is that D+ and D- are estimates with random error, so D+ is the estimated bound, with random error.
For example, it is not possible that only 10% of people pay more for red wine. It’s not possible because if only 10% of people paid more for red wine, then we would not see 30% more people paying more than $24 for red than for white, we would see at most a 10% increase, if everyone was in the sweetspot that values white <$24 and red >$24.
This is why we can bound the share showing the effect at 30%.
If 30% more people would pay $24 for red but not for white, then at least 30% of people would pay more for red wine. When you put it this way, it's kind of… …duh! (at least to someone who first thought of this 14 years ago).
Alright, but what if the dependent variable is continuous though? Can we still bound it?
Yes! And it's similarly intuitive. You dichotomize the DV, then do the same duh thing.
Say in our wine study we asked how much they would pay for either the red or the white wine, instead of asking only whether they would pay $24. So we get our data which is a bunch of dollar values instead of yesses and nos, some $29 here, some $7 there. How do we use dichotomization to find the bounds?
Say we dichotomize at $10. We compute how many dollar amounts are above and below that in the two conditions, and find that 80% of people pay $10 or more for red wine, and 55% for white wine. OK, so the duh thing tells us that then at least 25% of people pay more for red. Fine, but why $10? That was arbitrary. OK. We can try every possible price. Dichotomize at $1, then at $2, then at $3…. For each dichotomization you have one estimate, take the biggest of those numbers, and you have D+ from the KS test: the biggest vertical gap in the CDF. And hopefully you now see why that number bounds the share of people showing the effect, because my attempt at an explanation ends with this period.
This may feel p-hacky, the KS test is finding the cutoff by trying everything in the data. Well, it is p-hacky.
But the KS-test takes that into account when it computes its p-value, it adjusts for the 'multiple comparisons' so to speak. Indeed, it is usually considered a conservative test (under-rejects the null).
In Sum
The KS-test computes all the possible dichotomizations you could do of the dependent variable, and keeps track of the two dichotomizations producing the biggest differences between conditions in the cumulative shares of observations. These values, D+ and D- respectively, are bounds on the share of people influenced by the treatment positively and negatively.
Is this useful?
Maybe.
It’s a bound, so it will tend to be a low number. That is, the true value could be that 70% of people are influenced, and the bound could easily be just 20%. Bounds are like that. "At least 1 person will love this post" is not that informative a statement about how good this post is. So I lean to thinking this is more interesting than useful. Though it is an empirical question that depends on the shape of the distributions produced by treatments. I suspect it is potentially useful in two scenarios.
Scenario 1: when the majority of people in a study show an effect in one direction, but a minority of people show a strong effect in the opposite direction, and you care to realize this may be happening. For example, some antidepressants help most patients but exacerbate depression in a minority. The off-label Smirnov would be useful there to pick up that heterogeneity and prevent some disasters that have happened. So seems possibly useful for clinical trials (most people get less depressed, some people get very depressed)7would this be more or less useful than quantile tests? I don't know
Scenario 2: to remind us that when we show a difference of means we may be focusing on an effect that is shown by a minority of participants. If we got into the habit of reporting off-label KS, we may put more effort in determining whether our findings apply to most, some, or few people.
![]()
Author feedback
Our policy (.htm) is to share drafts of blog posts with authors whose work we discuss, in order to solicit suggestions for things we should change prior to posting, I emailed the authors of the Journal of Econometrics authors, but they did not reply. I did not contact Kolmogorov or Smirnov as they died in 1987 and 1966 respectively.