Last October, Science published the paper “Estimating the Reproducibility of Psychological Science” (htm), which reported the results of 100 replication attempts. Today it published a commentary by Gilbert et al. (.htm) as well as a response by the replicators (.htm).
The commentary makes two main points. First, because of sampling error, we should not expect all of the effects to replicate even if all of them were true. Second, differences in design between original studies and replication attempts may explain differences in results. Let’s start with the latter.[1]
Design differences
The commentators provide some striking examples of design differences. For example, they write, “An original study that asked Israelis to imagine the consequences of military service was replicated by asking Americans to imagine the consequences of a honeymoon” (p. 1037).
People can debate if such differences can explain the results (and in their reply, the replicators explain why they don’t think so). However, for readers to consider whether design differences matter, they first need to know those differences exist. I, for one, was unaware of them before reading Gilbert et al. (They are not mentioned in the 6 page Science article ..htm, nor 26 page supplement .pdf). [2]
This is not about pointing fingers, as I have also made this mistake: I did not sufficiently describe differences between original and replication studies in my Small Telescopes paper (see Colada [43]).
This is also not about taking a position on whether any particular difference is responsible for any particular discrepancy in results. I have no idea. Nor am I arguing design differences are a problem per-se, in most cases they were even approved by the original authors.
This is entirely about improving the reporting of replications going forward. After reading the commentary I better appreciate the importance of prominently disclosing design differences. This better enables readers to consider the consequences of such differences, while encouraging replicators to anticipate and address, before publication, any concerns they may raise. [3]
Noisy results
I am also sympathetic to the commentators' other concern, which is that sampling error may explain the low reproducibility rate. Their statistical analyses are not quite right, but neither are those by the replicators in the reproducibility project.
A study result can be imprecise enough to be consistent both with an effect existing and with it not existing. (See Colada[7] for a remarkable example from Economics). Clouds are consistent with rain, but also consistent with no rain. Clouds, like noisy results, are inconclusive.
The replicators interpreted inconclusive replications as failures, the commentators as successes. For instance, one of the analyses by the replicators considered replications as successful only if they obtained p<.05, effectively treating all inconclusive replications as failures. [4]
Both sets of authors examined whether the results from one study were within the confidence interval of the other, selectively ignoring sampling error of one or the other study.[5]
In particular, the replicators deemed a replication successful if the original finding was within the confidence interval of the replication. Among other problems this approach leads most true effects to fail to replicate with sufficiently big replication samples.[6]
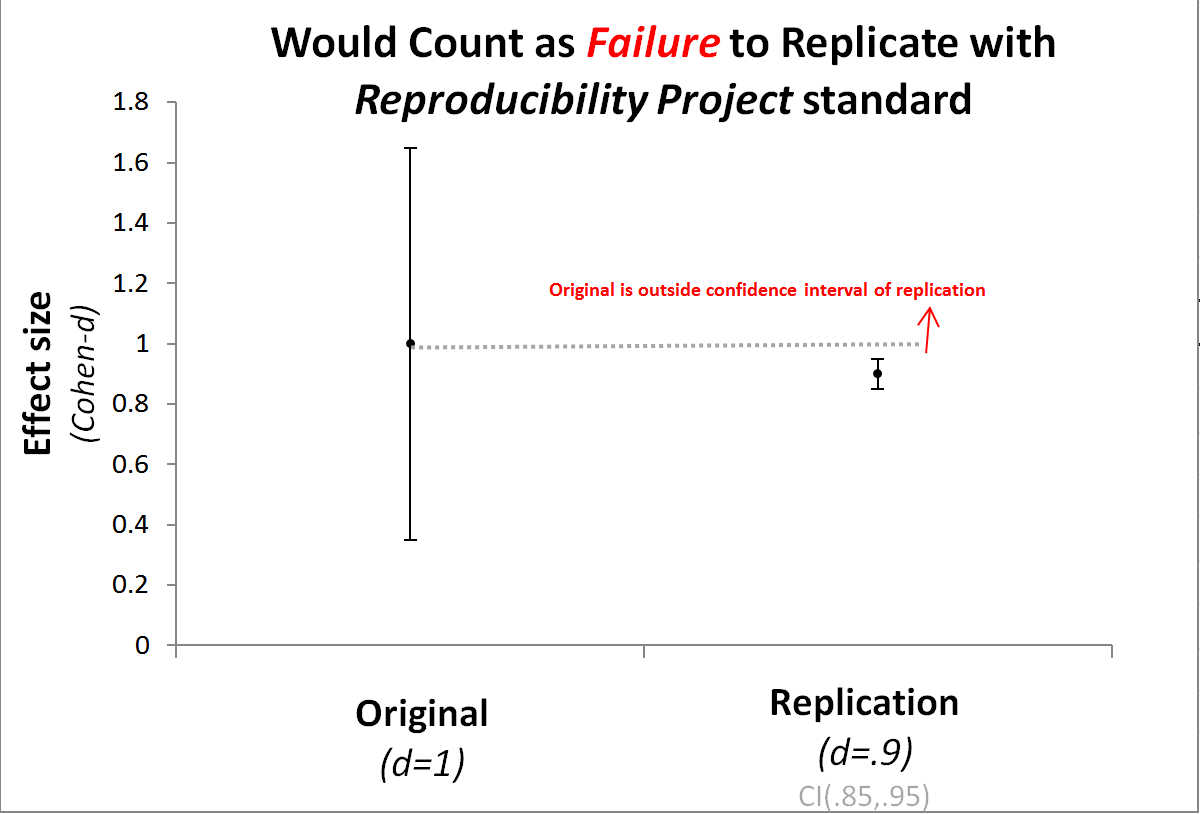
The commentators, in contrast, deemed replications successful if their estimate was within the confidence interval of the original. Among other problems, this approach leads too many false-positive findings to survive most replication efforts.[7]
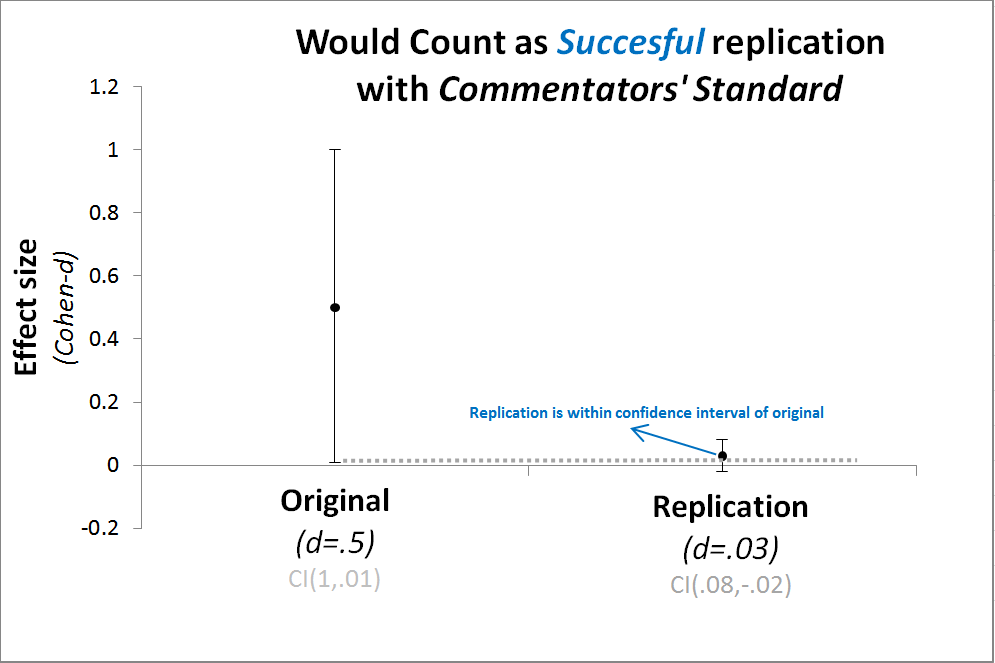
For more on these problems with effect size comparisons, see p. 561 in “Small Telescopes” (.pdf).
Accepting the null
Inconclusive replications are not failed replications.
For a replication to fail, the data must support the null. They must affirm the non-existence of a detectable effect. There are four main approaches to accepting the null (see Colada [42]). Two lend themselves particularly well to evaluating replications:
(i) Small Telescopes (.pdf): Test whether the replication rejects effects big enough to be detectable by the original study, and (ii) Bayesian evaluation of replications (.pdf).
These are philosophically and mathematically very different, but in practice they often agree. In Colada [42] I reported that for this very reproducibility project, the Small Telescopes and the Bayesian approach are correlated r = .91 overall, and r = .72 among replications with p>.05. Moreover, both find that about 30% of replications were inconclusive. (R Code). [8],[9]
40% full is not 60% empty
The opening paragraph of the response by the replicators reads:
“[…] the Open Science Collaboration observed that the original result was replicated in ~40 of 100 studies sampled”
They are saying the glass is 40% full. They are not explicitly saying it is 60% empty. But readers may be forgiven for jumping to that conclusion, and they almost invariably have. This opening paragraph would have been equally justified:
“[…] the Open Science Collaboration observed that the original result failed to replicate in ~30 of 100 studies sampled”
It would be much better to fully report:
“[…] the Open Science Collaboration observed that the original result was replicated in ~40 of 100 studies sampled, failed to replicate in ~30, and that the remaining ~30 replications were inconclusive.”
Summary
1. Replications must be analyzed in ways that allow for results to be inconclusive, not just success/fail
2. Design differences between original and replication should be prominently disclosed.
Author feedback.
I shared a draft of this post with Brian Nosek, Dan Gilbert and Tim Wilson, and invited them and their co-authors to provide feedback. I exchanged over 20 emails total with 7 of them. Their feedback greatly improved, and considerably lengthened, this post. Colada Co-host Joe Simmons provided lots of feedback as well. I kept editing after getting feedback from all of them, so the version you just read is probably worse and surely different from the versions any of them commented on.
Concluding remarks
My views on the state of social science and what to do about it are almost surely much closer to those of the reproducibility team than to those of the authors of the commentary. But. A few months ago I came across a "Rationally Speaking" podcast (.htm) by Julia Galef (relevant part of transcript starts on page 7, .pdf) where she talks about debating with a "steel-man" version, as opposed to straw-man, of an argument. It changed how I
approach disagreements. For example, the Gilbert et al commentary opens with what appears to be an incorrectly calculated probability. One could straw-man argue against the commentary by focusing on that calculation. But the argument such probability is meant to support does not hinge on precisely estimating it. There are other weak-links in the commentary, but its steel-man version, the one focusing on its strengths rather than weaknesses, did make me think better about the issues at hand and ended up with what I think is an improved perspective on replications.
We are greatly indebted to the collaborative work of 100s of colleagues behind the reproducibility project, and to Brian Nosek for leading that gargantuan effort (as well as many other important efforts to improve the transparency and replicability of social science). This does not mean we should not try to improve on it or to learn from its shortcomings.
Footnotes.
- The commentators actually focus on three issues: (1) (Sampling) error, (2) Statistical power, and (3) Design differences. I treat (1) and (2) as the same problem [↩]
- However, the 100 detailed study protocols are available online (.htm), and so people can identify them by reading those protocols. For instance, here (.htm) is the (8 page) protocol for the military vs honeymoon study. [↩]
- Brandt et al (JESP 2014) understood the importance of this long before I did, see their 'Replication Recipe' paper .htm [↩]
- Any true effect can fail to replicate with a small enough sample, a point made in most articles making suggestions for conducting and evaluating replications, including Small Telescopes (.pdf). [↩]
- The original paper reported 5 tests of reproducibility: (i) Is the replication p<.05?, (ii) Is the original within the confidence interval of the replication?, (iii) Does the replication team subjectively rate it as successful vs failure? (iv) Is the replication directionally smaller than the original? and (v) Is the average of original and replication significantly different from zero? In the post I focus only on (i) and (ii) because: (iii) is not a statistic with evaluative properties (but in any case, also does not include an ‘inconclusive bin’), and neither (iv) nor (v) measure reproducibility. (iv) Measures publication bias (with lots of noise), and I couldn’t say what (v) measures. [↩]
- Most true findings are inflated due to publication bias, so the unbiased estimate from the replication will eventually reject it [↩]
- For example, the prototypically p-hacked p=.049 finding, has a confidence interval that nearly touches zero. To obtain a replication outside that confidence interval, therefore, we need to observe a negative estimate. If the true effect is zero, that will happen only 50% of the time, so about half of false-positive p=.049 would survive replication attempts [↩]
- Alex Etz in his blog post did the Bayesian analyses long before I did and I used his summary dataset, as is, to run my analyses. See his PLOS ONE paper, .htm. [↩]
- The Small Telescope approach finds that only 25% of replications conclusively failed to replicate, whereas the Bayesian approach says this number is about 37%. However, several of the disagreements come from results that barely accept or don't accept the null, so the two agree more than these two figures suggest. In the last section of Colada[42] I explain what causes disagreements between the two. [↩]