Of all economics papers published this century, the 10th most cited appeared in Economics Letters , a journal with an impact factor of 0.5. It makes an inconvenient and counterintuitive point: the sign of the estimate (b̂) of an interaction in a logit/probit regression, need not correspond to the sign of its effect on the dependent variable (Ai & Norton 2003, .pdf; 1467 cites).
That is to say, if you run a logit regression like y=logit(b1x1+b2x2+b3x1x2), and get b̂3= .5, a positive interaction estimate, it is possible (and quite likely) that for many xs, the impact of the interaction on the dependent variable is negative; that is, that as x1 gets larger, the impact of x2 on y gets smaller [1].
This post provides an intuition for that reversal, and discusses when it actually matters.
side note: Many economists run "linear probability models" (OLS) instead of logits, to avoid this problem. But that does not fix this problem, it just hides it. I may write about that in a future post.
Buying a house (no math)
Let’s say your decision to buy a house depends on two independent factors: (i) how much you like it (ii) how good an investment it is.
Unbounded scale. If the house decision were on an unbounded scale, say how much to pay for it, liking and investment value would remain independent. If you like the house enough to pay $200k, and in addition it would give you $50k in profits, you’d pay $250k; if the profits were $80k instead of $50k, then pay $280k. Two main effects, no interaction [2].
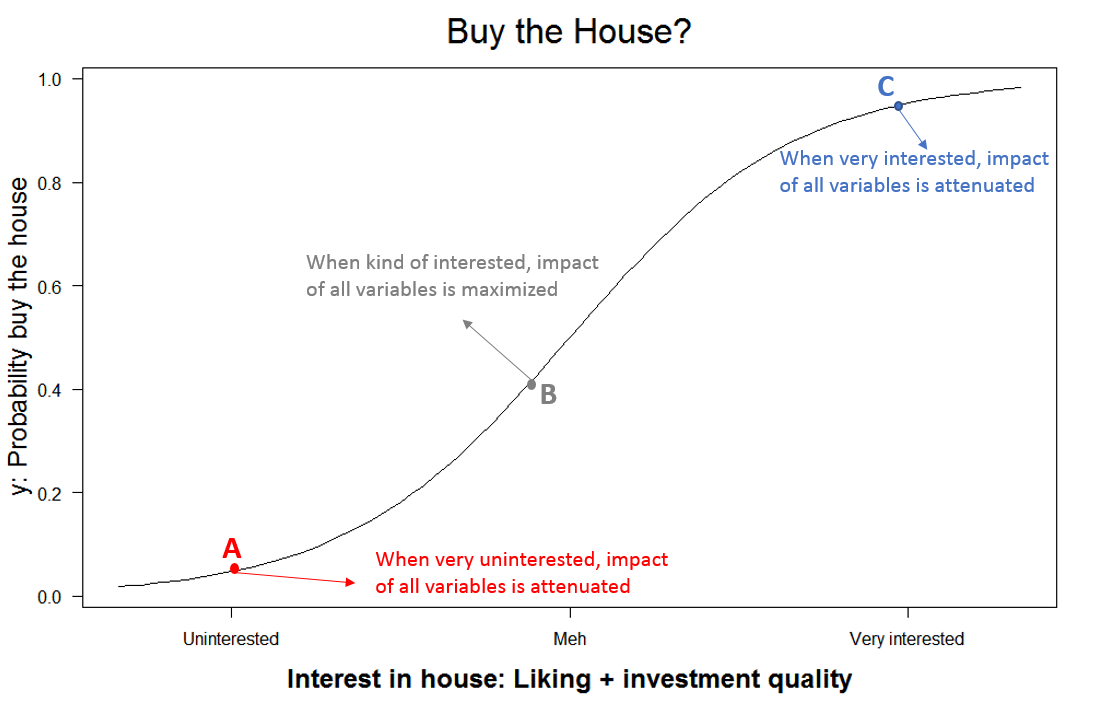
Bounded scale. Now consider, instead of $ paid, measuring how probable it is that you buy the house; a bounded dependent variable (0-1). Imagine you love the house (Point C in figure below). Given that enthusiasm, a small increase or drop in how good an investment it is, doesn’t affect the probability much. If you felt lukewarm, in contrast (Point B), a moderate increase in the investment quality could make a difference. And in Point A, moderate changes again don’t matter much.
Key intuition: when the dependent variable is bounded [3], the impact of every independent variable moves it closer/further from that bound, and hence, impacts how flat the curve is, how sensitive the dependent variable it is to changes in any other variable. Every variable, then, has an interactive effect on all variables, even if they are not meaningfully related to one another and even if interaction effects are not included in the regression equation.
Mechanical vs conceptual interactions
I call interactions that arise from the non-linearity of the model, mechanical interactions, and those that arise from variables actually influencing each other, conceptual interactions.
In life, most conceptual interactions are zero: how much you like the color of the kitchen in a house does not affect how much you care about roomy closets, the natural light in the living room, or the age of the AC system. But, in logit regressions, EVERY mechanical interaction is ≠0; if you love the kitchen enough that you really want to buy the house, you are far to the right in the figure above and so all other attributes now matter less: closets, AC system and natural light all now have less detectable effects on your decision.
In a logit regression, the b̂s one estimates, only capture conceptual interactions. When one computes “marginal effects”, when one goes beyond the b̂ to ask how much the dependent variable changes as we change a predictor, one adds the mechanical interaction effect.
Ai and Norton’s point, then, is that the coefficient may be positive, b̂>0, conceptual interaction positive, but the marginal effect negative, conceptual+mechanical negative.
Let’s take this to logit land
Let
y: probability of buying the house
x1: how much you like it
x2: how good an investment it is
and,
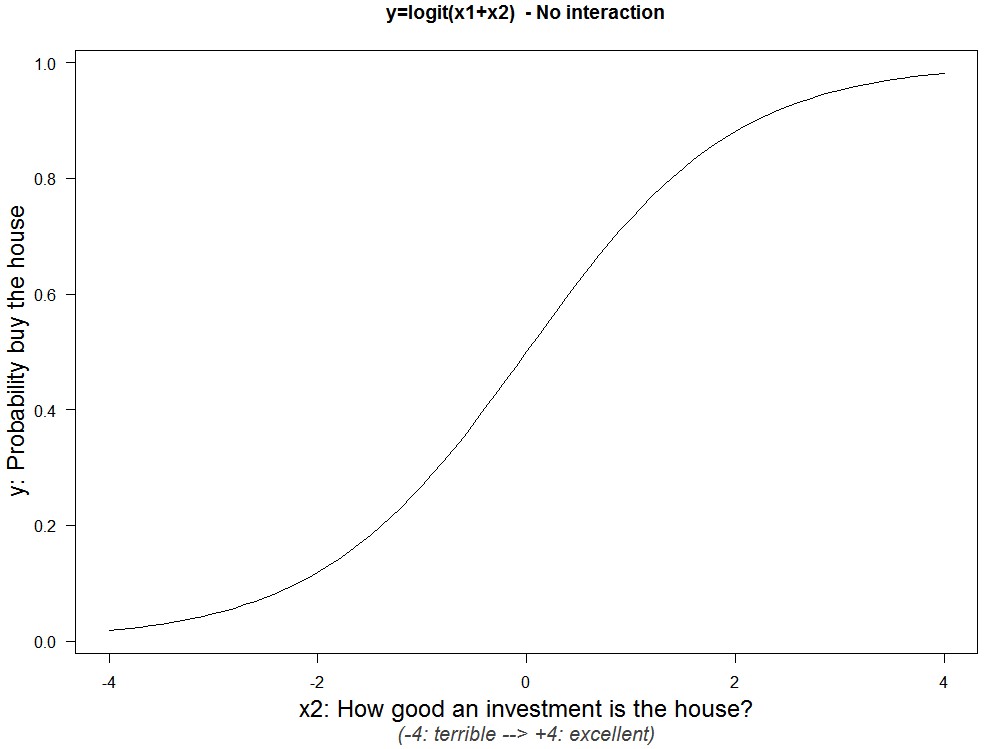
y= logit(b1x1+b2x2) [4]
(note: there is no interaction in the true model, no x1x2 term)
Below I plot that true model, y on x2, keeping x1 constant at x1=0 (R Code for all plots in post).
We are interested in the interaction of x1 with x2. On how x2 affects the impact of x1 on y. Let’s add a new line to the figure, keeping x1 fixed at x1=1 instead of x1=0.
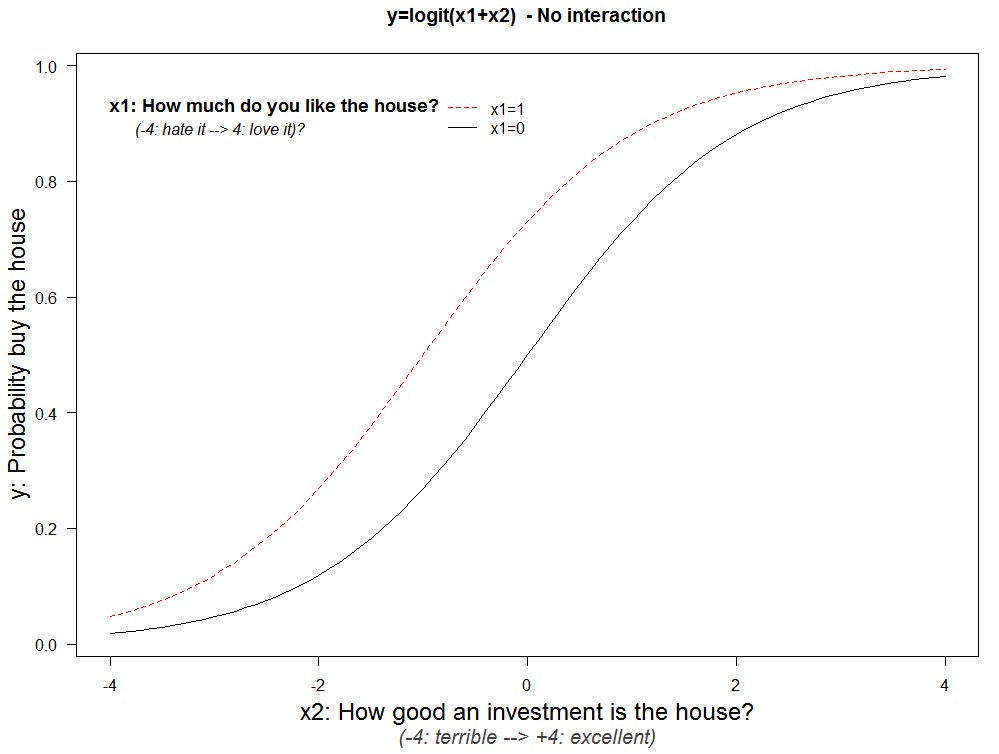
For any given investment value, say x2=0, you are more likely to buy the house if you like it more (dashed red vs solid black line). The vertical distance between lines is the impact of x1=1 vs x1=0; one can already see that around the extremes the gap is smaller, so the effect of x1 gets smaller when x2 is very big or very small.
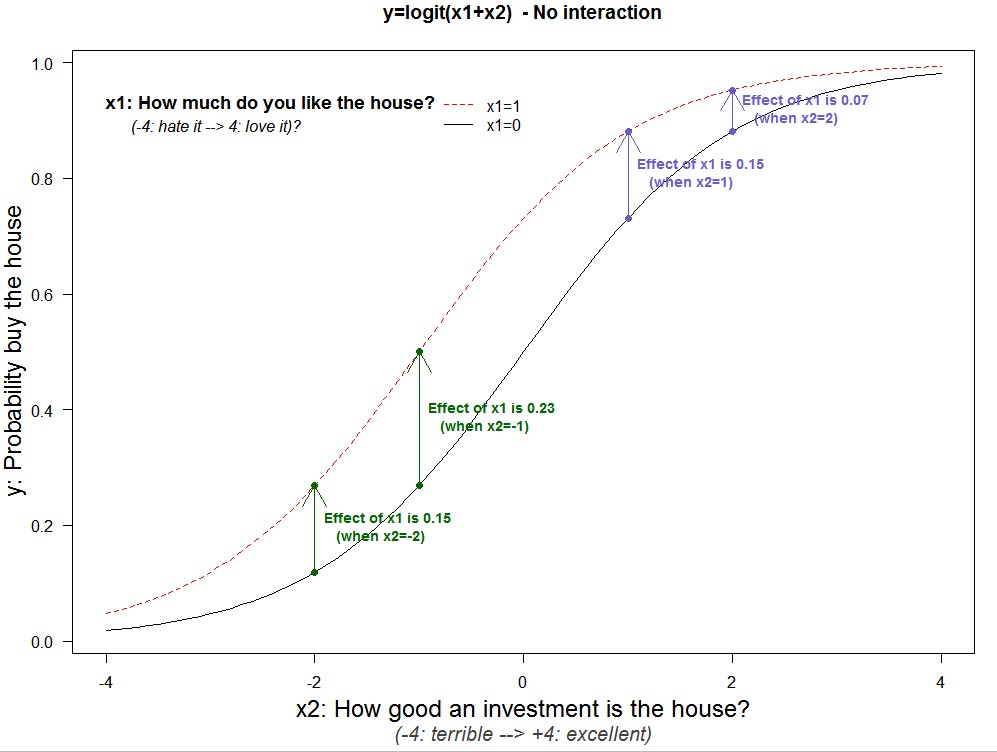
Below I add arrows that quantify the vertical gaps at specific x2 values. For example, when x2=-2, going from x1=0 to x1=1 increases the probability of purchase by 15%, and by 23% when x2=-1 [5]
The difference across arrows captures how the impact of x1 changes as we change x2; the interaction. The bottom chart, under the brackets shows the results. Recall there is no conceptual interaction here, model is y=x1+x2, so those interactions, +.08 and -.08 respectively, are purely mechanical.
Now: the sign reversal
So far we assumed x1 and x2 were not conceptually related. The figure below shows what happens when they are: y=logit(x1+x2+0.25x1x2). Despite the conceptual interaction being b=.25 > 0, the total effect of the interaction is negative for high values of x2 (e.g., from x2=1 to x2=2, it is -.08); the mechanical interaction dominates.
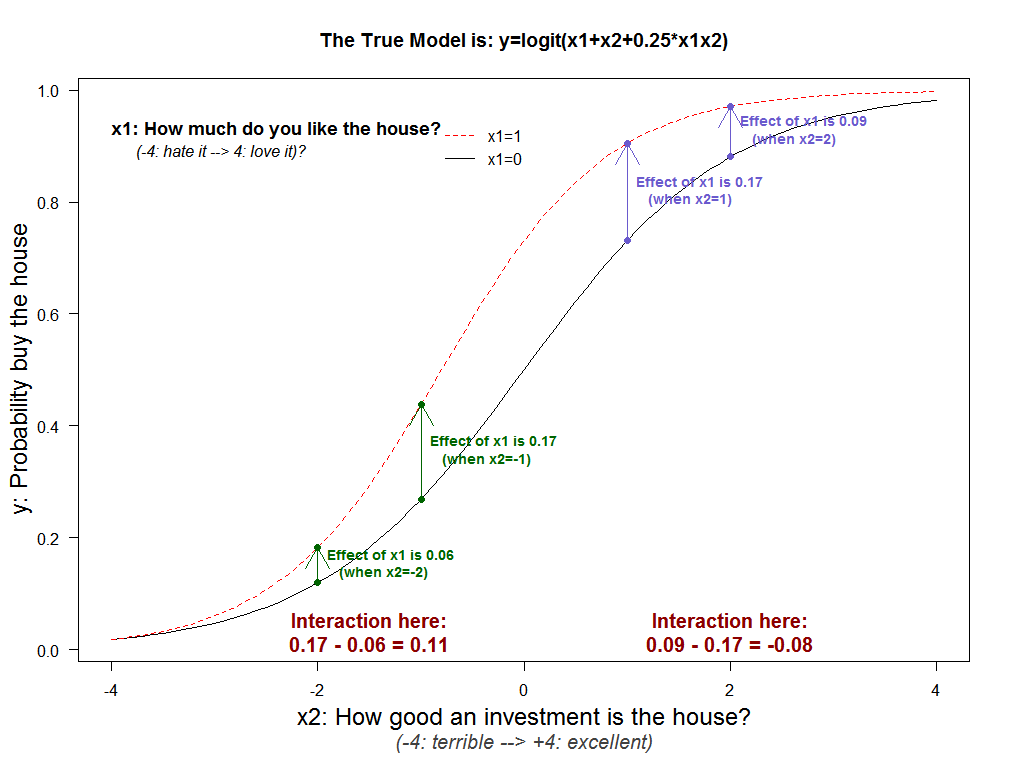
What to do about this?
Ai & Norton propose not focusing on point estimates at all, not focusing on b̂3=.25. To instead compute how much the dependent variable changes with a change of the underlying variables, the marginal effect of the interaction, the one that combines conceptual and mechanical. To do that for every data-point, and reporting the average.
In another Econ Letters paper, Greene (2010; .pdf) [6] argues averaging the interaction is kind of meaningless. He has a point, ask yourself how informative it is to tell a reader that the average interaction effect depicted above, +.11 and -.08, is +.015. He suggests plotting the marginal effect for every value instead.
But, such graphs will combine conceptual and mechanical interactions. Do we actually want to do that? It depends on whether we have a basic-research or applied-research question.
What is the research question?
Imagine a researcher examining the benefits of text-messaging parents of students who miss a homework and that the researcher is interested on whether messages are less beneficial for high GPA student (so on the interaction: message*GPA).
An applied research question may be:
How likely is a student to get an A in this class if we text message his parents when missing a homework?"
For that question, yes, we need to include the mechanical interaction to be accurate. If high GPA students were going to get an A anyway, then the text-message will not increase the probability for them. The ceiling effect is real and should be taken into account. So we need the marginal effect.
A (slightly more) basic-research question may be:
How likely is a student to get more academically involved in this class if we text message his parents when missing a homework?
Here grades are just a proxy, a proxy for involvement; if high GPA students were getting an A anyway, but thanks to the text-message will become more involved, we want to know that. We do not want the marginal effect on grades, we want the conceptual interaction, we want b̂.
In sum: When asking conceptual or basic-research questions, if b̂ and the marginal effects disagree, go with b̂.
![]()
Authors feedback.
Our policy is to contact authors whose work we discuss, asking to suggest changes and reply within our blog if they wish. I shared a draft with Chunrong Ai & Edward Norton. Edward replied indicating he appreciated the post and suggested I tell readers about another article of his, further delving into this issue (.pdf)
- note: logit here stands for code syntax, logit regression, rather than math syntax, logit function [↩]
- What really matters is linear vs non-linear scale rather that bounded vs not, but bounded provides the intuition more clearly. [↩]
- As mentioned before, the key is non-linear rather than bounded [↩]
- the logit model is y=eb1x1+b2x2/(1+e b1x1+b2x2) . [↩]
- percentage points, I know, but it’s a pain to write that every time. [↩]
- The author of that “Greene” Econ PhD econometrics textbook .htm [↩]