In a recent referee report I argued something I have argued in several reports before: if the effect of interest in a regression is an interaction, the control variables addressing possible confounds should be interactions as well. In this post I explain that argument using as a working example a 2011 QJE paper (.htm) that examined domestic violence following NFL games.
I chose that paper because it provides an intuitive setting to explain the need for interaction controls, and because it is the paper that first prompted me to think of this issue (several years ago).
The 2011 QJE paper
This excerpt from the abstract summarizes the key finding:

Codebook.
Pregame point spread: Number of points the favorite team is expected to win by.
Local viewing audience: How many locals watched the game on TV.
Table IV in the paper has the key result:
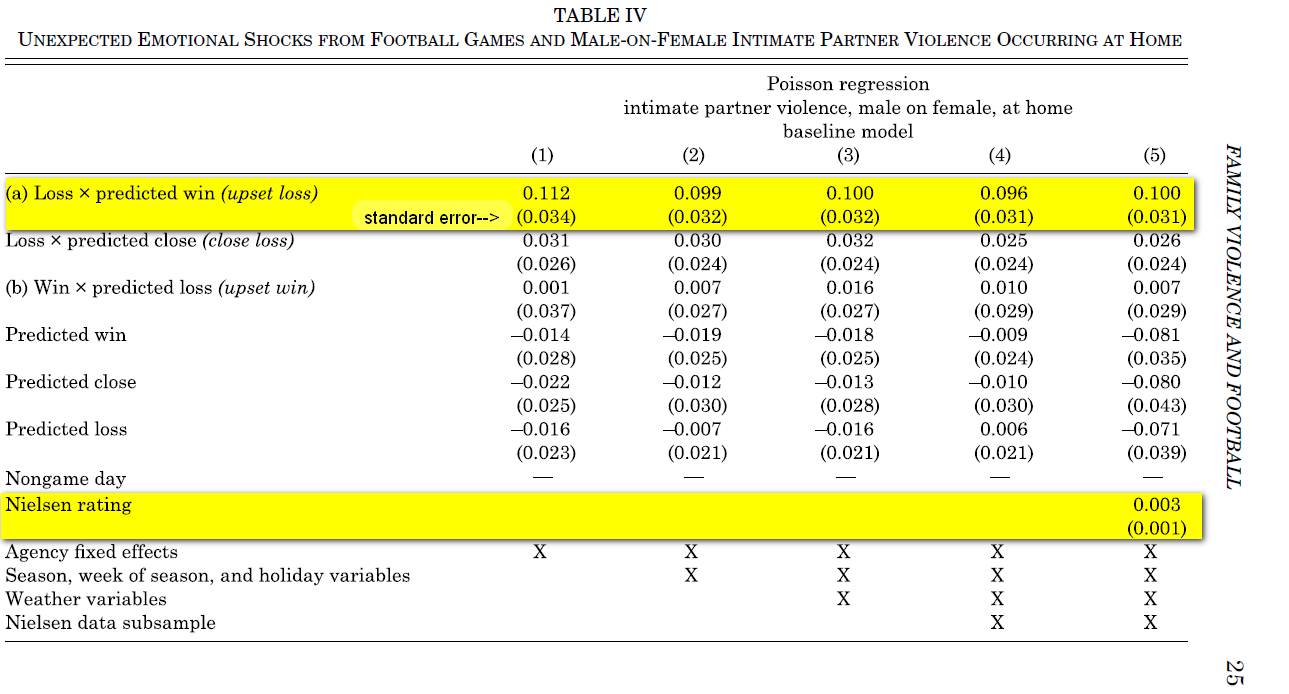
Each column is a different (Poisson) regression with domestic violence after an NFL game as the dependent variable. As we move right the regressions include more controls.
The first row shows the estimated effect of a surprising vs. expected loss. The point estimate is about 0.10, corresponding to that 10% increase in violence mentioned in the abstract (scroll up).
Viewership: a confound that worried the original authors
As the QJE paper notes, one concern with the finding is that more people watch games when their team is expected to win (see footnote for details of the authors’ original discussion of this issue [1]). This means that more people watch surprising losses than watch expected losses. We thus have two explanations for greater violence after surprising losses:
Explanation 1: surprising losses are more enraging.
Explanation 2: surprising losses are watched by more people.
Column (5) in Table IV above intends to tease these two apart by controlling for viewership (the "Nielsen rating" row). But the point of this post is that such control is not sufficient.
If the confound we were worried about was that the bigger the number of fans watching any game, the more violence there is, then controlling for the Nielsen rating as a main effect would be the right solution. But we are concerned with something different. The confound we are worried about is that the bigger the number of fans watching a loss, the more violence there is.
More generally, because the effect of interest is an interaction, any alternative explanation for it must also involve an interaction. In this particular case, the effect of interest involves an interaction with the team losing, and therefore, any confound must also involve an interaction with the team losing. So we want viewership to potentially have a different effect for games won vs lost, so we need to add the term Nielsen Rating*Loss as a predictor.
I make the same point with simple regression equations in this footnote [2].
This is a relatively common issue.
I browsed the last two issues of some top economic journals (AEJ:Applied, AER, & QJE) and found several papers with regressions where an interaction effect was of interest, and where controls to address confounds were included. But I did not find any that included interaction-controls. The need for interaction-controls does not seem to be an issue applied researchers are generally aware of.
Punchline.
When the coefficient of interest is an interaction, and confounds are a concern, interacted controls are needed.
![]()
Author feedback
Our policy (.htm) is to share drafts of blog posts that discuss someone else's work with them to solicit suggestions for things we should change prior to posting. I shared a draft with David Card and Gordon Dahl. They did not suggest any changes but Gordon reported the results with the suggested interaction controls, writing [I added the approximate p-values in [ ] for readers who may be interested in them]:
"adding these interactions does not appreciably change the point estimate on the upset loss variable: it becomes .095 (.056) [approx. p-value=.09]. This compares to the estimates reported in the QJE paper of .100 (.0310) [approx. p-value <.001] when we only control for Nielsen rating and .096 (.031) when we don't control for Nielsen rating at all. Interestingly, the coefficients on rating*loss and rating*win are almost identical: .0031 versus .0034, respectively. Moreover, our test for loss aversion (upset loss = – upset win) has a p-value of .02 now, whereas before it was .01. So our conclusion is that adding in the interaction terms with ratings results in less precise estimates, but doesn't change the estimates appreciably."
I thank David and Gordon for their time, and for dusting off the STATA code from nearly 10 years ago for this post.
Shortly after this post went live, Dominique Muller (@dom_muller) alerted me to this JESP (.htm) paper dealing with this very issue and documenting that psychology papers don't include interaction controls.
Footnotes.- Discussion by QJE 2011 authors of role of viewership.
Section III.D in the paper deals with the viewership issue in two paragraphs. The authors note that a regression predicting viewership with ex-ante spread implies that going from a -4 to a +4 spread implies just a 1 percentage point increase in viewership and thus “we infer that any differential reaction to the outcomes of predicted wins versus predicted losses is unlikely to be attributable to changes in viewership.” (p.124). This seems sensible to me and a reasonable guess in the absence of a better way of addressing this issue, but, including an interaction control of viewership with loss vs gain is a better way of addressing it. [↩] - Presenting the problem with generic regression equations.
Say a paper is interested in an interaction between x & z, the term c in (1)(1) y=ax+bz+cxz,
When authors are concerned that a third variable, w, is correlated with x, and correlated with y, then, to account for this confound, it is not enough to estimate (2),
(2) y=ax+bz+cxz+dw
Instead, one must estimate (3),
(3) y=ax+bz+cxz+dw+ewz
The 2011 QJE paper, and the several papers I have reviewed that motivated this post, estimated (2).
<end of Colada[80]> [↩]
