There is a 2019 paper, in the journal Political Analysis (htm), with over 1000 Google cites, titled "How Much Should We Trust Estimates from Multiplicative Interaction Models? Simple Tools to Improve Empirical Practice". The paper is not just widely cited, but is also actually influential. Most political science papers estimating interactions now-a-days, seem to rely on the proposed simple tools.1According to the Web-of-Science this is the 3rd most cited article with the phrase "How Much Should We Trust… " in the title, beating 15 other papers
In this post I explain why those tools should not be used with observational data.
Notation
We are interested in situations where the effect of the focal predictor, x, on a dependent variable, y, is possibly impacted by a moderator, z, and we examine this possibility with a regression like y=a+bx+cz+dxz.
The original paper
The Political Analysis paper identifies two problems with how researchers in its field interpret regression results to compute the effect of x on y at given values of z.
Problem 1. Reporting effect of x for extreme, sometimes impossible values of z.
Problem 2. Neglecting the possibility that the interaction may be non-linear.
The paper introduces two tools to address both problems: the "binning estimator" and the "kernel estimator". The article also mentions that it can be useful to make 3D surface plots with GAMs (p.8; appendix).
The tool that gets the most attention, both in their paper, and in empirical work citing it, is the "binning estimator". For example, the article has been cited in three AJPS articles in 2024, all three use (only) the binning estimator. 2 The three 2024 AJPS articles citing the paper and using the binning estimator are
https://doi.org/10.1111/ajps.12835
https://doi.org/10.1111/ajps.12852
https://doi.org/10.1111/ajps.12868
There is a fourth article that cites but does not actually mention the Political Analysis paper at all: https://doi.org/10.1111/ajps.12836
The binning estimator starts by forming three data subsets, bins, with low, medium, and high values of z. It then estimates y= a+bx+cz+dxz separately in each bin. It then reports back the estimated effect of x on y for the median value of z in each bin. So, we get three effect size estimates of x, one for low, one for medium, and for high z values.
The figure below, from the Political Analysis paper, illustrates the output of the binning estimator side-by-side that of a linear regression, in a simulated dataset where the true effect is linear.
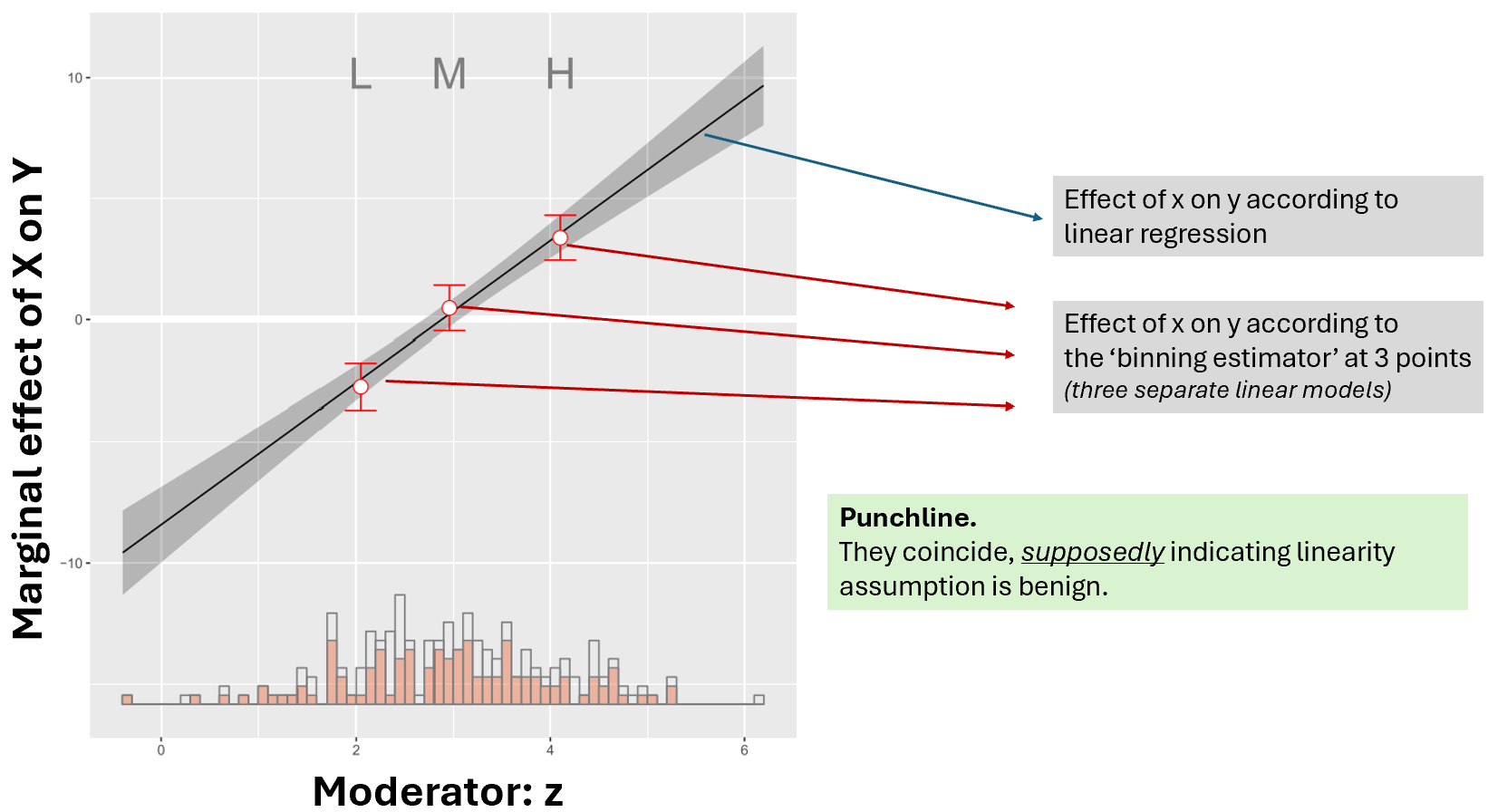 Fig 1. Annotated Figure 2a in the Political Analysis paper
Fig 1. Annotated Figure 2a in the Political Analysis paper
I added arrows and colored boxes, and also relabeled the axes.
The Political Analysis paper re-analyzes data from various published papers, in some the binning estimator gave similar results to the linear regression, in others less so. For instance:
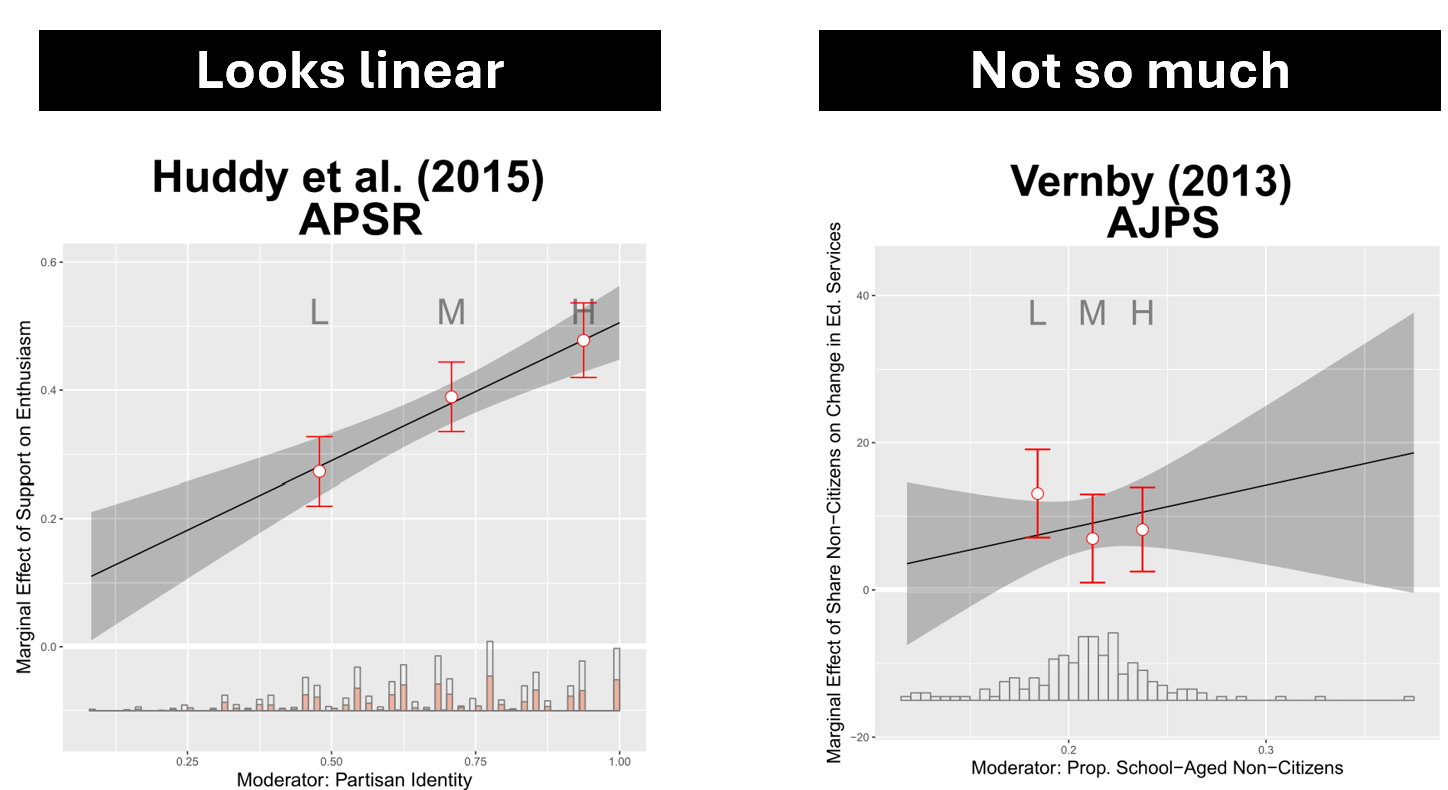 Fig 2. Two of many plots shown in Figure 8 in the Political Analysis paper
Fig 2. Two of many plots shown in Figure 8 in the Political Analysis paper
Note: black boxes with white text added for this post.
An overlooked problem
The Political Analysis article overlooked a third problem that can heavily bias interactions in linear models. This third problem is less intuitive than the ones they attend to, and more importantly, it biases also the binning estimator. (This third problem was discussed in a few psych papers in the 1990s that are not as influential as I think they should be). 3The best among them, in my view, is Ganzach (1997) "Misleading interaction and curvilinear terms", Psychological methods (.htm)
The third problem is that if x and z in that x·z interaction are correlated, and either x or z impacts y non-linearly, the estimate of interaction term, d, in y=a+bx+cz+dxz is biased, and the binning estimator from the Political Analysis paper is also biased, possibly by the same amount.
Most notably, one is likely to find false-positive interactions, and marginal effects of the wrong sign.
I next provide an illustration, then the intuition.
Illustration
Let's make the example as simple as possible.
Recall that the problem arises if either x or z affect y non-linearly, and if x & z are correlated. So let's make the true model simple and non-linear, y=x2+e, and r(x,z)=.5.
Let's then estimate the regression y= a+bx+cz+dxz .
In reality, z is not part of the true model, but because of its correlation with x, the estimated linear model will, incorrectly, conclude it's in the model, and moreover, that it interacts with x.
We see in the figure that the linear regression believes the effect of x on y increases linearly with z, and we see that the binning estimator is like, "amen brother".
Fig 3. Correlated Non-Linear Predictors Produce a Spurious Linear Interaction
R Code to reproduce figure: https://researchbox.org/2063/7 (Code: PLPFAX)
Note: On 2025 03 05 this figure was updated fixing a few misleading or erroneous labels
Please see https://datacolada.org/123 for a more in depth discussion of the underlying issues.
The intuition for Problem 3
I don't think it's intuitive why the estimate of the x·z interaction is biased when x and z are correlated. So here I try to provide an intuition. A useful framework is "omitted variable bias".
Omitted variable bias arises when a regression omits a predictor that correlates both with the dependent and the independent variable(s). A classic example is that if you run a regression predicting drownings with ice-cream consumption, without controlling for seasonality or temperature, you get a biased estimate.
Studying interactions assuming the effects of x and z on y are linear, is equivalent to omitting the non-linear portions of the effects of x and z from the regression. Variables in the regression that correlate with the omitted nonlinearities of x or z will have biased estimates. And, that is the case with the x·z interaction.
The simple quadratic example above makes the simile to omitted variable bias literal, as we are literally omitting the term x2 from the regression; because z is correlated with x, it follows that z·x is correlated with x·x, the omitted x2 term. Thus x·z is biased by the omitted variable x2.
It may seem surprising that the binning estimator is also biased because it seems like it does not assume linearity. But, it does. Within each bin, the effects of x and z on y enter linearly as predictors. Omitted nonlinearities within bins produce bias within bins.
The solution: GAM instead
Generalized Additive Models, GAMs, like linear regressions, estimate the effect of predictors on a dependent variable, but GAMs estimate rather than assume functional form. 4GAM is similar to local regression (LOESS), and Kernel regression, but performs better (in accuracy and computational cost), and is more scalable (e.g., to incluce covariates or nested data).
I have a paper, "interacting with curves" (.pdf), proposing using GAMs for testing and probing interactions. That paper needs at least an entire separate blogpost to be covered, so here I just point out that the tool I propose there, "GAM Simple Slopes", gets it right in Figure 3 here. .
300 illustrations
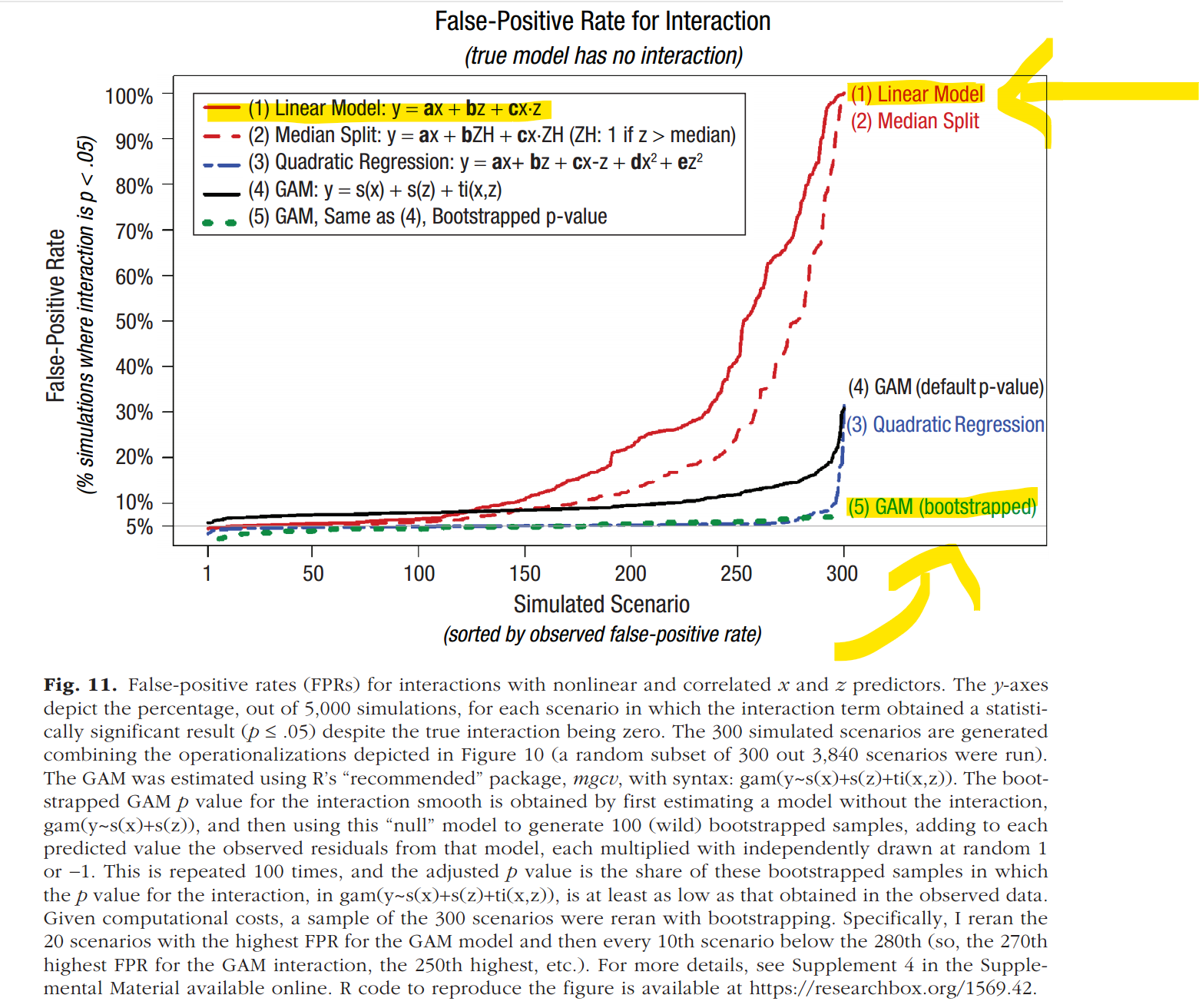
In my 'interacting with curves' (.pdf) paper I simulated 300 different scenarios (different sample sizes, distributions, functional forms, etc), where there is a non-linear effect of x and z on y, but no xz interaction, and I assess how often different tools get a false-positive interaction (the linear model did awful, the GAM great).
For this post i went back to the R Code behind those simulations and I assessed how well the binning estimator did. It was quite wrong quite often, in several scenarios it had false-positive rates above 70%.
You just read rejected arguments.
About a year ago I submitted a commentary (.pdf) to the original journal, Political Analysis, with the concerns expressed here (it was longer and contained additional points; for example, that also for experimental data the binning estimator is worse than GAM, because it has less power. When the true model is linear, confidence intervals are about 10% wider with the binning estimator than with GAM). The paper was rejected in the first round of reviews. I asked Jeff Gill, the editor writing the rejection letter, whether I could post the reviews here. He was quite clear that I shouldn't. So you will have to trust my characterization of the review provided by my peers: most notable, nobody challenged the validity of the statistical argument, nobody challenged that the binning estimator, a method currently endorsed by Political Analysis to address non-linearities, is biased by non-linearities.
Summary
The binning estimator
1) Provides less information (estimating the effect at three single points, instead of all possible points)
2) Has a (sometimes extremely) elevated false-positive rate
3) Has less power
4) Is just as easy to estimate as are the "GAM Simple Slopes", both require a single line of code:
binning: interflex::interflex(method='binning', y,x,z)
GAM: interacting::interprobe(x,z,y)
In a nutshell: Binning is a dominated strategy.
Read more:
1. Published "interacting with curves" paper (.pdf)
2. Rejected "don't bin, GAM instead" preprint( .pdf)
3. Github page with {interacting} pkg (.htm)
![]()
Author feedback
Our policy (.htm) is to share drafts of blog posts with authors whose work we discuss, in order to solicit suggestions for things we should change prior to posting, I emailed the authors of the Political Analysis paper and they raised four main points that I tried to address, including adding the false-positive simulations, making explicit they mention GAMs in their paper, and dropping some terms they objected to.
Update February 13th
On February 11th, Jonathan Mummolo sent me an email forwarding a tweet announcing they had written a response to this post and posted the 26 page document (with two new authors) to arxiv.org, and asking I link to it from here. I indicated I needed 3 days to read their paper as was quite busy, and that I wanted to consider whether it may merit, instead of just a link, a new post discussing it. Mummolo adamantly opposed I do anything but link to it here (sending me a photograph of our feedback policy from our website) and indicating I should follow it as is. His co-author, Yiqing Xu followed up separately writing that "I felt your engagement with our initial private exchange was insufficient and selective".
I asked the authors to provide:
- an explanation for not having indicated when I sent them the final draft of this post that they felt my response was insufficient
- A justification for having not reciprocated me sharing the draft before posting and instead having notified me of their response only after they announced it on social media, and
- For concrete evidence that I was selective and insufficient in my response to feedback.
If they answer these requests I will post them here.
The link to their response/paper which as of this writing I still have not had a chance to read let alone think critically about: .pdf