A recent Science-paper (.html) used a total sample size of N=40 to arrive at the conclusion that implicit racial and gender stereotypes can be reduced while napping.
N=40 is a small sample for a between-subject experiment. One needs N=92 to reliably detect that men are heavier than women (SSRN). The study, however, was within-subject, for instance, its dependent variable, the Implicit Association Test (IAT), was contrasted within-participant before and after napping. [1]
Reasonable question: How much more power does subtracting baseline IAT give a study?
Surprising answer: it lowers power.
Design & analysis of napping study
Participants took the gender and race IATs, then trained for the gender IAT (while listening to one sound) and the race IAT (different sound). Then everyone naps. While napping one of the two sounds is played (to cue memory of the corresponding training, facilitating learning while sleeping). Then both IATs are taken again. Nappers were reported to be less biased in the cued IAT after the nap.
This is perhaps a good place to indicate that there are many studies with similar designs and sample sizes. The blogpost is about strengthening intuitions for within-subject designs, not criticizing the authors of the study.
Intuition for the power drop
Let’s simplify the experiment. No napping. No gender IAT. Everyone takes only the race IAT.
Half train before taking it, half don’t. To test if training works we could do
Between-subject test: is the mean IAT different across conditions?
If before training everyone took a baseline race IAT, we could instead do
Mixed design test: is the mean change in IAT different across conditions?
Subtracting baseline, going from between-subject to a mixed-design, has two effects: one good, one bad.
Good: Reduce between-subject differences. Some people have stronger racial associations than others. Subtracting baselines reduces those differences, increasing power.
Bad: Increase noise. The baseline is, after all, just an estimate. Subtracting baseline adds noise, reducing power.
Imagine the baseline was measured incorrectly. The computer recorded, instead of the IAT, the participant’s body temperature. IAT scores minus body temperature is a noisier dependent variable than just IAT scores, so we’d have less power.
If baseline is not quite as bad as body temperature, the consequence is not quite as bad, but same idea. Subtracting baseline adds the baseline’s noise.
We can be quite precise about this. Subtracting baseline only helps power if baseline is correlated r>.5 with the dependent variable, but it hurts if r<.5. [2]
See the simple math (.html). Or, just see the simple chart.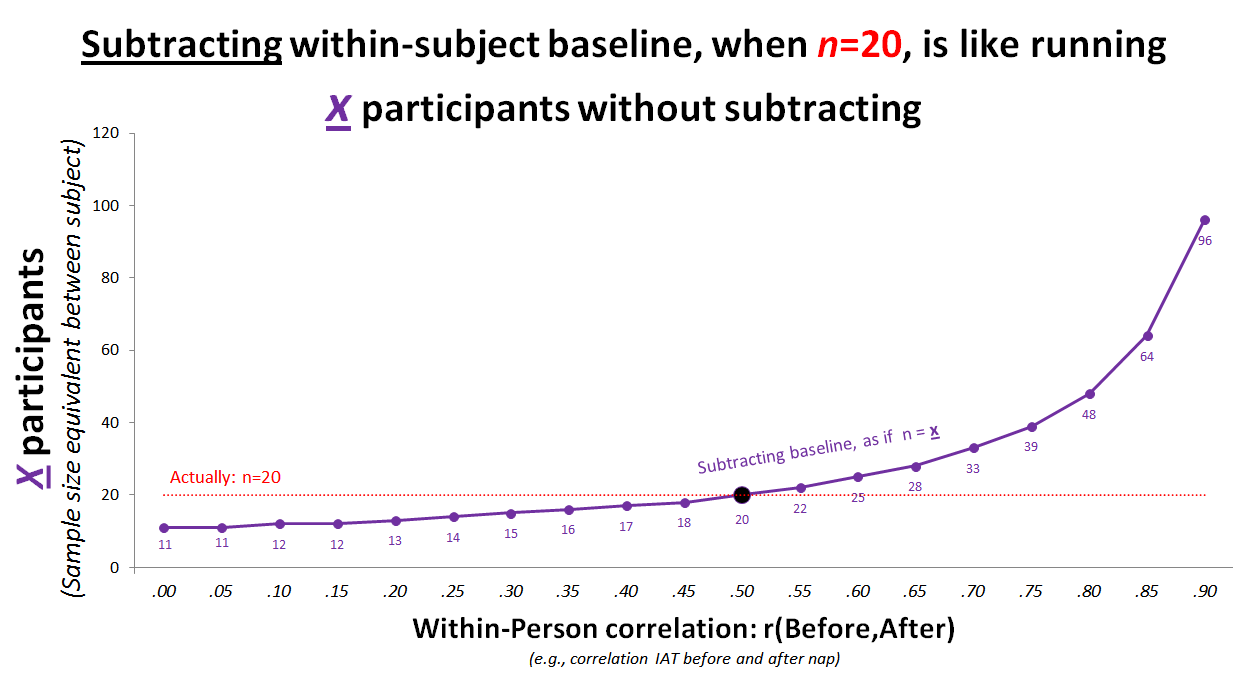 
e.g., running n=20 per cell and subtracting baseline, when r=.3, lowers power enough that it is as if the sample had been n=15 instead of n=20. (R Code)
Before-After correlation for IAT
Subtracting baseline IAT will only help, then, if when people take it twice, their scores are correlated r>.5. Prior studies have found test-retest reliability of r = .4 for the racial IAT. [3] Analyzing the posted data (.html) from this study, where manipulations take place between measures, I got r = .35. (For gender IAT I got r=.2) [4]
Aside: one can avoid the power-drop entirely if one controls for baseline in a regression/ANCOVA instead of subtracting it. Moreover, controlling for baseline never lowers power. See bonus chart (.pdf).
Within-subject manipulations
In addition to subtracting baseline, one may carry out the manipulation within-subject, every participant gets treatment and control. Indeed, in the napping study everyone had a cued and a non-cued IAT.
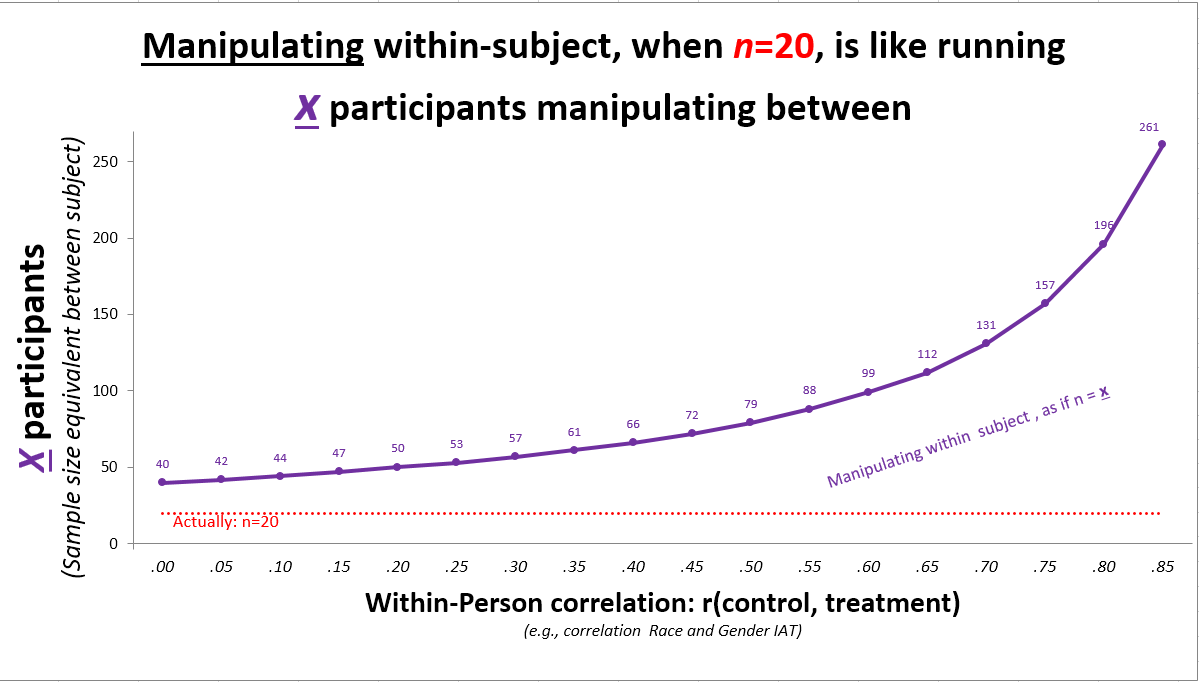
How much this helps depends again on the correlation of the within-subject measures: Does race IAT correlate with gender IAT? The higher the correlation, the bigger the power boost.
note: Aurélien Allard, a PhD student in Moral Psychology at Paris 8 University, caught an error in the R Code used to generate this figure. He contacted me on 2016/11/02 and I updated the figure 2 days later. You can see the archived version of the post, with the incorrect figure, here.
When both measures are uncorrelated it is as if the study had twice as many subjects. This makes sense. r=0 is as if the data came from different people, asking two questions from n=20 is like asking one from n=40. As r increases we have more power because we expect the two measure to be more and more similar, so any given difference is more and more statistically significant (R Code for chart) [5].
Race & gender IATs capture distinct mental associations, measured with a test of low reliability, so we may not expect a high correlation. At baseline, r(race,gender)=-.07, p=.66. The within-subject manipulation, then, "only" doubled the sample size.
So, how big was the sample?
The Science-paper reports N=40 people total. The supplement explains that actually combines two separate studies run months apart, each N=20. The analyses subtracted baseline IAT, lowering power, as if N=15. The manipulation was within subject, doubling it, to N=30. To detect “men are heavier than women” one needs N=92. [6]
Author feedback
I shared an early draft of this post with the authors of the Science-paper. We had an extensive email exchange that led to clarifying some ambiguities in the writing. They also suggested I mention their results are robust to controlling instead of subtracting baseline.
Footnotes.
- The IAT is the Implicit Association Test and assesses how strongly respondents associate, for instance, good things with Whites and bad things with Blacks; take a test (.html) [↩]
- Two days after this post went live I learned, via Jason Kerwin, of this very relevant paper by David McKenzie (.html) arguing for economists to collect data from more rounds. David makes the same point about r>.5 for a gain in power from, in econ jargon, a diff-in-diff vs. the simple diff. [↩]
- Bar-Anan & Nosek (2014, p. 676; .html); Lane et al. (2007, p. 71; .pdf) [↩]
- That’s for post vs pre nap. In the napping study the race IAT is taken 4 times by every participant, resulting in 6 before-after correlations. Raning -.047 to r = .53; simple average r = .3. [↩]
- This ignores the impact that going from between to within subject design has on the actual effect itself. Effects can get smaller or larger depending on the specifics. [↩]
- The idea of using men-vs-women weight as a benchmark is to give a heuristic reaction; effects big enough to be detectable by the naked eye require bigger samples than the ones we are used to seeing when studying surprising effects. For those skeptical of this heuristic, let's use published evidence on the IAT as a benchmark. Lai et al (2014 .pdf) run 17 interventions seeking to reduce IAT scores. The biggest effect among these 17 was d=.49. That effect size requires n=66 per cell, N=132 total, for 80% power (more than for men vs women weight). Moderating this effect through sleep, and moderating the moderation through cueing while sleeping, requires vastly larger samples to attain the same power. [↩]