This is the third post in a series (.htm) in which we argue/show that meta-analytic means are often meaningless, because they often (1) include invalid tests of the hypothesis of interest to the meta-analyst and (2) combine incommensurate results. The meta-analysis we discuss here explores how dishonesty differs across four different experimental paradigms (e.g., coin flips vs. die rolls). As you will see below, even studies that share such a simple design – like studies that ask participants to privately flip a coin and assess whether they dishonestly report the result – are so different that they cannot be meaningfully compared or combined.
To make this post a manageable length, this critique narrowly focuses on one small part of the published meta-analysis. The published article includes quite a few more analyses and results than we discuss below, including analyses that explore how individual differences and experimental attributes correlate with dishonesty.
In this post we discuss a 2019 Psychological Bulletin paper entitled “The Truth About Lies: A Meta-analysis on Dishonest Behavior” (.htm). In this paper, the authors’ primary goal was to determine whether different experimental paradigms “come to the same or different conclusions about dishonest behavior.”
To accomplish this, the authors analyzed 558 studies of dishonesty [1]. To make things simple, we’ll focus entirely on “coin-flip tasks” (n = 163 effect sizes) and “die-roll tasks” (n = 129 effect sizes) [2]. The meta-analysts define a “coin-flip task” as one that has 2 possible outcomes (e.g., heads or tails) and a “die-roll task” as one that has more than 2 outcomes (e.g., each side of a six-sided die). This can be confusing, because, for example, “coin-flip tasks” don’t have to involve coin flips (and can even involve die rolls!), but we’ll walk you through it.
The paper reports a few different results but we’ll focus on just one of them:
People are more likely to lie in die-roll tasks (52%) than in coin-flip tasks (30%).
The meta-analysts reached this conclusion by comparing the percentage of liars in the average die-roll study to the percentage of liars in the average coin-flip study. For details, see this footnote: [3].
In this post, we will analyze four studies contained in this meta-analysis, two studies that were coded as “everybody lied” and two studies that were coded as “nobody lied”. We will start with the “everybody lied” studies, and consider whether they really did find that everybody lied. We will then discuss the “nobody lied” studies, and consider whether the results of die-roll studies and coin-flip studies can be meaningfully compared.
Before getting started there are two additional things to know. First, the meta-analysis focuses on selfish dishonesty; people who lied in a way that did not materially benefit them were coded as “honest.” Second, “each experimental condition was counted as one experiment” (p. 8). So if a study had 5 conditions, then it was counted as 5 different studies. Statistically speaking, this is totally fine so long as different conditions are statistically independent.
Studies In Which Everybody Lied
Did Everybody Lie In This “Coin-Flip” Study?
The meta-analysis includes one coin-flip study that was coded as indicating that everybody lied: Study 4 of a 2015 paper published in the Journal of Research in Personality (.htm). Confusingly, this study involved a die roll but was coded as a coin-flip study because, like a coin flip, the outcome was dichotomous.
German student participants first chose which of two die-roll games to play. Then they played the game they chose and won some money if the outcome of the die roll matched a pre-determined number; otherwise they did not win anything [4]:
Game 1: Impossible-to-Cheat Game: Participants roll the die in front of the experimenter, winning 2 euros if they roll a pre-determined number.
Game 2: Possible-to-Cheat Game: Participants roll the die in private, winning 1 euro if they claim to roll a pre-determined number.
Note that it would be super weird to choose the “Possible-to-Cheat” game and then to not cheat; doing so lowers their possible earnings from 2€ to 1€ . It is rational to choose the “Possible-to-Cheat” game only if you plan to cheat.
The “100% dishonesty” result reflects the fact that 100% of those who chose the “Possible-to-Cheat” game did, in fact, cheat. Clearly this is not a valid measure of the full sample’s level of dishonesty. No matter what percentage of participants are willing to cheat, it will always be true that ~100% of those who chose to cheat will cheat. A more meaningful measure of dishonesty would be “the percentage of participants who chose to play the “Possible-to-Cheat’ game”, which was 47% [5].
Did Everybody Lie In These “Die Roll” Studies?
The meta-analysis includes six die-roll results that were coded as finding that 100% of people were dishonest. Two of those results come from the same 2015 paper, published in the Journal of Behavioral and Experimental Economics (.htm). German students from the University Duisberg-Essen privately flipped a coin four times and then reported how many flips came up tails. They were paid 1 euro for every tails they reported. (Confusingly, because there are more than 2 outcomes – the number of reported tails (out of 4) – this coin flipping exercise counts as a “die-roll task” in the meta-analysis.)
The study had four experimental conditions, two of which were coded as finding 100% dishonesty. In the “Lab sample” condition (n = 60), participants reported their coin flip results during a lab session via a web form. In the “Home sample” condition (n = 66), participants did the same thing, but “could access the [web form] via the internet from home” (p. 89) [6].
The following chart shows the proportion of participants reporting 0, 1, 2, 3, and 4 tails in each condition. The red bars show the proportion that was expected if all participants reported honestly.
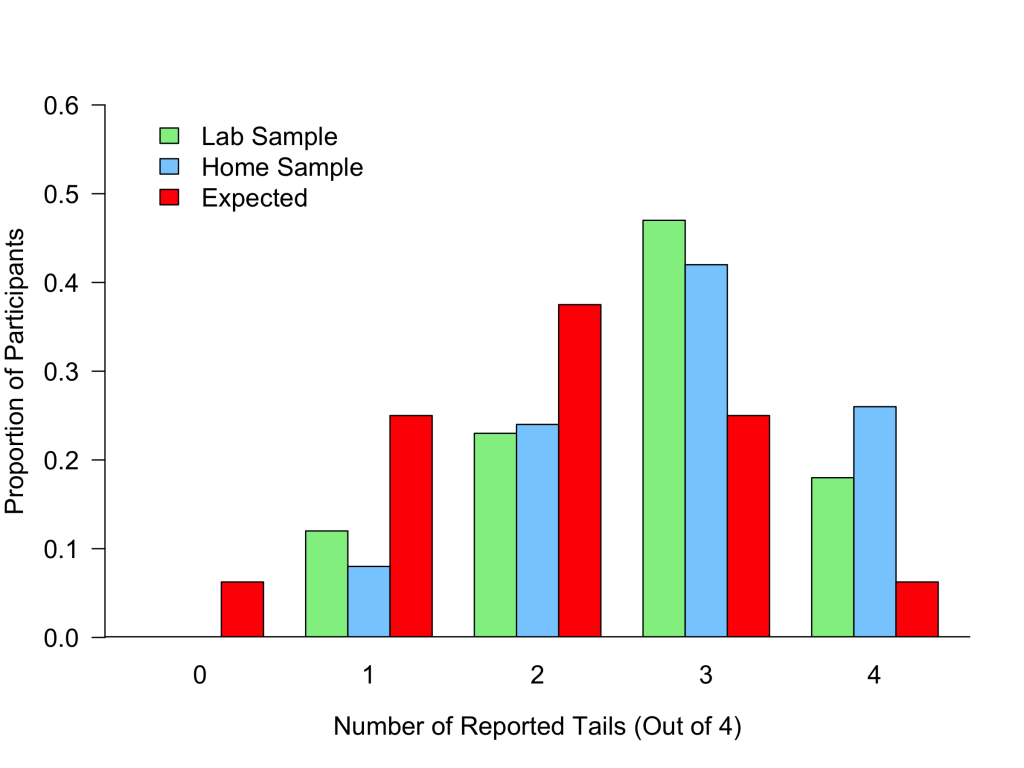
You can see that participants in these two conditions reported more 3 and 4 tails than would be expected by chance. It is clear that some participants were dishonest.
But how many? According to the meta-analysts, the answer is that 100% of participants were dishonest. Everybody lied. Is that true?
It’s actually hard to know. Did everyone who reported 1 tail actually observe 0 tails, did everyone who reported 2 tails actually observed fewer than 2 tails, etc. To navigate this difficulty, the meta-analysts made a choice: “For die-roll tasks, the rate of liars was calculated using only reports of the lowest possible outcome” (p. 8, emphasis ours), comparing the percentage of people who reported to the lowest possible outcome to the percentage that would be expected if everyone were honest. The meta-analysts were effectively saying, “We can’t tell from distributions like these exactly how many people lied, but we do know that those who reported zero tails did not lie, so let’s focus on that.” Because no participants reported zero tails, there were no unambiguously honest people, and so they coded this as 100% dishonesty [7].
We understand the logic, but it does suffer from some important shortcomings. Most notably, because it relies on a very small sliver of the distribution, the estimate of “percentage of dishonest people” is very noisy. For example, for the Lab Sample condition, the expected number of people reporting 0 tails is only ~4 out of 60 (.54*60 = 3.75), so the meta-analysts’ estimate of 100% dishonesty is based on what ~4 people are expected to do. Although the fact that no participants reported 0 tails is consistent with 100% dishonesty, it is also consistent with other possibilities. Indeed, it wouldn’t surprise us if the truth were that “only” 3 out of 4 (75%) or 2 out of 4 (50%) of people were dishonest. As an analogy, if a political pollster interviews four randomly selected voters, and all of them say they will vote for the Democrat, it would not be safe to conclude that everyone is voting for the Democrat. Indeed, it would not even be safe to conclude that the Democrat will win.
In addition to the noise problem, the reliance on small samples may also magnify a bias in favor of concluding that honest people are actually dishonest. See footnote for details: [8].
These concerns also apply to the other four “everybody-lied” die-roll studies in the meta-analysis, all of which come from the same paper published in the Journal of Economic Behavior & Organization in 2018 (.htm). In addition, the meta-analysts made a coding error that inflated dishonesty estimates for two of these studies (see footnote: [9]).
Interim Conclusion
The evidence presented in this section suggests that the meta-analytic estimates of “100% dishonesty” may not be 100% accurate. This critique applies to one “everybody lied” coin-flip study and to six “everybody lied” die-roll studies. We take this to mean that the percentage of liars has probably been overstated, and more so for the die-roll studies than the coin-flip studies. Obviously, it would take more than an audit of such a small number of studies to see how consequential this is overall.
Studies In Which Nobody Lied
Nuns
The meta-analysts report five die-roll studies in which nobody lied. In the interest of space, we’ll describe just one of them, from a 2013 paper in the Journal of Economic Behavior & Organization (.htm).
The key result comes from, um, 12 Franciscan nuns who privately rolled a six-sided die and reported the outcome. The higher the reported outcome, the more the nun got paid, except a report of “6” meant that she earned zero. A profit-seeking nun would have benefitted from falsely reporting a “4” or a “5” and by not reporting a “6”. But no nun reported a “4” or a “5”, and 16.7% reported a “6”, exactly how many 6s would be expected by chance.
The evidence suggests that the Franciscan nuns didn’t lie, at least not in a direction that benefited themselves [10].
Would Greeks Lie For A Lindt? How About Austrians? Or Indonesians? Or…
The meta-analysis includes 14 coin-flip cases of 0% dishonesty (i.e., no lying at all). One of these comes from Pascual-Ezama et al. (2015; .htm), who asked 15 U.K. participants to privately flip a black/white coin and to then report the result. If they reported “white” they received a Lindt chocolate; otherwise they received nothing. For one variant of this study, the results implied that 0% of the people lied.
Why would so few people lie? Maybe because they are good people. Or maybe they just didn’t want the chocolate. The vast majority of people need an incentive to lie. In this study maybe the incentive wasn’t sufficient.
At this point, it’s worth having a conversation with you, the reader:
YOU: “OK, well this seems like a valid study, and so why should I be concerned about its inclusion in this meta-analysis?”
COLADA: “We agree that the study is probably valid, but recall that the coin-flip studies exhibited lower levels of dishonesty than the die-roll studies. If the coin-flip studies happen to offer lower incentives to lie (e.g., an unwanted chocolate), then maybe that’s one reason why coin-flip-task dishonesty is lower. That is, it might not be the coin-flip-ness that is causing lower dishonesty, but rather the reduced incentives to lie.
YOU: “OK, yeah, but surely you can’t draw that conclusion because of a single study that features potentially low incentives to lie.”
COLADA: “We agree. On the other hand, if it were not a single study, then we should get proportionally more concerned.”
Here’s a screenshot of a sorted portion of the meta-analysts’ dataset, showing the 14 coin-flip studies (out of 163) in which, statistically speaking, nobody lied [11]. We’d ask if you notice anything, but our highlighting gives it away:
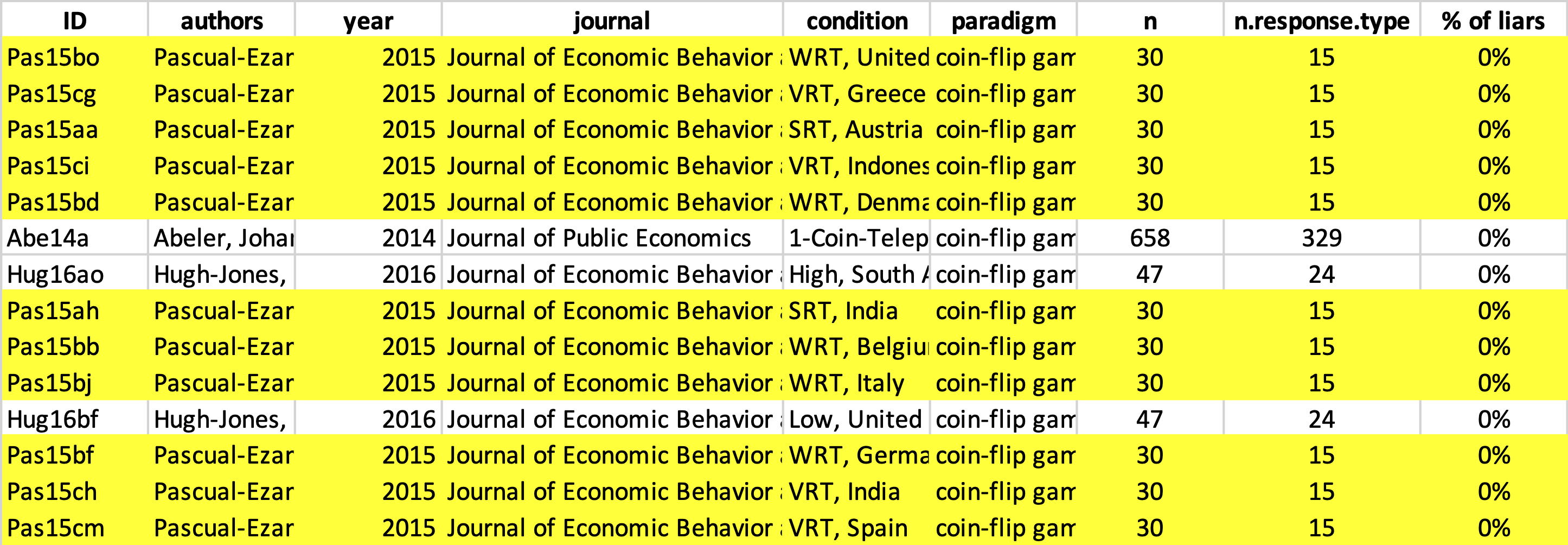
Right. So 11 of the 14 (78.5%) coin-flip studies that were coded as "nobody lied" come from this one paper. So, yeah, this study wasn’t conducted once. Turns out that it was conducted in 16 different countries, under 3 different (but similar) conditions. So the willingness to lie for a chocolate is in the meta-analysis 48 times. Across all 48 variations, people lied 18% of the time.
The choice to include these independent conditions as 48 distinct experiments is not wrong, but it is a choice – one that gives this paper 48 times the weight it might otherwise have – and it is consequential. If instead of including it 48 times, the authors included it only once (averaging across all 48 “conditions”), the average rate of dishonesty in the coin-flip studies would increase from 30% to 35%. The meta-analysts’ largely arbitrary decision of how to code a single paper decreases the dishonesty gap between coin-flip studies and die-roll studies by ~23% [12]. There is no right or wrong way to solve this issue, because there is no true proportion of Lindt-chocolate studies in the population. The problem is not with the meta-analysts’ coding decisions. The problem is with the enterprise as a whole, with taking an arbitrary sample of studies that happened to have been conducted, averaging their results, and interpreting that average as something meaningful [13].
To drive this point home, consider that some studies are going to find low levels of selfish lying. For example, studies run on Franciscan nuns and studies that tempt you to lie to procure a (measly?) chocolate. If you run a bunch of such low-dishonesty studies using coin flips but not using die rolls, you’ll be more likely to find that people are more honest in coin-flip paradigms. But if you instead do the opposite, and run a bunch of such low-dishonesty studies using die-rolls but not coin-flips, well, you’ll be more likely to find the opposite: that people are more honest in die-roll paradigms.
Meta-analytic averages are not (meaningfully) capturing what happens at the center of some platonic distribution of “dishonesty in coin-flip tasks”, because that distribution does not exist (see Colada [33] .htm). They are (meaninglessly) capturing what researchers happened to do. And if they happened to do different things in coin-flip tasks than in die-roll tasks, well, then you’re likely to find different results in coin-flip tasks than in die-roll tasks. And that meta-analyzed difference has no meaning.
Conclusions
Many meta-analysts not only want to generate an average effect size, they want to compare effect sizes across some feature or attribute (e.g., comparing the effects of behavioral “nudges in academic vs. non-academic contexts (.htm), or dishonesty in coin-flipping vs. die tasks.)
Now if you want to simply document a historical correlation and say something like, “In the past researchers have, on average, observed more dishonesty in die-roll studies than in coin-flip studies,” then, yes, knock yourself out and do a meta-analysis (but please correct the inaccurate estimates and remove the invalid studies.) But if you want to go beyond the recording of history and learn about causal effects that inform our understanding of human psychology or the effectiveness of interventions, then this type of meta-analytic enterprise is not going to cut it.
As experimental researchers, we try to design studies that prevent or handle confounds. We try to ensure that the groups we are comparing differ only in what we care about. To learn if coin flipping or die throwing leads to more lying, we randomly assign a given pool of participants to do one or the other, matching tasks on everything that matters (e.g., incentives, instructions, whether participants are nuns, etc). This is Research Methods 101.
But somehow once the word “meta-analysis” is put in front of us, it’s like everything we learned (or even teach!) in Research Methods 101 temporarily exits our brain, replaced by the mantra that “meta-analysis is the gold standard”. We ignore the fact that coin-flip tasks and die-roll tasks may differ in all sorts of ways – not only in the psychology the tasks evoke in participants, but in whether those studies are run on economics students or nuns, in whether the incentive to lie is small or large, in how dishonesty is coded, etc. But we trust analyses that compare them as though they were on equal footing.
To be clear, we believe that these meta-analysts have done a better job than most at being careful, at being transparent, and at acknowledging some of the limitations (e.g., saying things like “experimental manipulations would be required to infer causality about when and why people shy away from overreporting”, p. 20). But such acknowledgements do not communicate the depth of the problem. The studies that are being compared differ so dramatically that, well, they can’t really be compared. All it takes to meaningfully alter the stated conclusion is for someone to run a bunch more die-roll studies on Franciscan nuns.
![]()
Author feedback:
Our policy (.htm) is to share drafts of blog posts with authors whose work we discuss, in order to solicit suggestions for things we should change prior to posting, and to invite them to write a response that we link to at the end of the post. We contacted the authors of the meta-analysis, and the authors of the 5 individual papers we discussed.
1) The authors of the meta-analysis were very professional and responsive. They provided this thoughtful response:
Meta-analyses are often criticized for comparing apples to oranges and ours is no exception. We share Data Colada’s concern about invalid interpretation and inaccurate usage of single results from large meta-analyses. We invite researchers to read our meta-analysis carefully and examine the extensive analyses we conducted in an effort to understand the data beyond mean differences (e.g., how incentives, demographics and other variables affect dishonesty within and between experimental paradigms, when other sources of variation are controlled for).
The Data Colada post focuses on one result based on one measure, rate of liars. This was not the main measurement of our meta-analysis (rather, the “standardized report” was). As we noted in our paper, there is a unique problem with estimating the rate of liars in random-outcomes tasks (i.e., what we call die-roll and coin-flip tasks), despite its widespread use. We thank the Data Colada team for elaborating this point further. Indeed, estimates of this rate will become unreliable if relatively few participants observe the lowest outcome. In addition, we agree that the lower bound of 0 rates of liars may lead to a biased estimate.
We also thank Data Colada for their close inspection of our data set. Despite our efforts to ensure accuracy, we miscoded two of the four conditions of Andersen et al. (2018) and included Study 4 of Hilbig and Zettler (2015), even though the self-selection mechanisms it implemented made it unsuitable. In response to these valuable observations, we sent Psychological Bulletin an updated data file with the above corrections and the grouping variable for our multi-level analysis, which accounted for dependency between studies.
Importantly, even when correcting the data set, allowing for negative rates of liars, including only studies with at least 20 participants who were estimated to observe the lowest outcome and accounting for statistical dependency, the difference in the rates of liars between coin-flip tasks (30%) and die-roll tasks (50%) amounts to a difference of 20 percentage points. The paper reported a difference of 22 percentage point.
To conclude, the qualitative result we reported in the paper seems robust, probably due to the large number of studies and participants. But, as is argued in the post, this result represents only the experimental parameters and manipulations of the studies in the field up to the time point of the meta-analysis. Yes, the grand means are partly based on different frequencies of specific incentive/population types. Acknowledging this possibility, we believe that the best way to advance causal knowledge in this domain is through controlled studies. In a recent paper, two of us explicitly called for such systematic manipulations to understand what properties of the paradigms or contextual variables (e.g., no elasticity in coin-flip tasks vs. elasticity in die-roll tasks) cause the differences (Gerlach & Teodorescu, 2022, .htm).
We are of the view that while meta-analyses may inform subsequent experimental studies of potential variables that should be investigated further, they rarely offer definitive results and final answers.
2) Sebastian Berger, corresponding author on the “Lab”- vs. “Home”-sample study, said that he “shared [our] criticism of the meta-study." Ben Hilbig, the first author of paper featuring the Possible- vs. Impossible-To-Cheat game, provided very helpful feedback (see Footnote 5). Julie Marx, corresponding author of the "everybody lied" studies described in Footnote 9, signed off on the post. David Pascual-Ezama, first author of the paper that included 48 variations of the Lindt chocolate study, provided very helpful feedback that led us to improve the precision and accuracy of our post. Most notably, David emphasized to us that his coin-flip studies did not necessarily find that nobody lied in those 14 variations, just that the aggregated statistics happened to be consistent with that conclusion. Indeed, on the whole, Pascual-Ezama et al. (2015) found significant evidence of dishonesty. Moreover, a more recent paper first-authored by David (.htm) – and published after this meta-analysis (and thus not included) – showed that individual dishonesty could be present even when aggregated data don’t show it. No other authors or teams of authors responded to our request for feedback.
Footnotes.
- The paper’s abstract and public significance statement say that the authors used data from “565 experiments”, but the body of the paper (e.g., Figure 1) and the posted dataset indicate that 558 results were analyzed. [↩]
- The meta-analysis also analyzes “matrix” tasks and “sender-receiver” tasks. We focus on coin-flip and die-roll tasks because they are easier to understand and describe. [↩]
- So if there are two die-roll studies, and everybody lies in one of them and nobody lies in the other, then the percentage of liars in the average die-roll study would be 50%. Because the authors used random effects, this average is computed *across studies* – every study gets roughly equal weight – and trivially depends on sample size and not at all on study design, etc. Indeed, although random effects meta-analyses involve some fancy math what it is actually doing is averaging across studies while largely ignoring the differences among those studies. We’ll run into an interesting consequence of this when we get to our last example. [↩]
- We have re-named the games for expository purposes. In the original article, these games are referred to as “open” and “concealed”, respectively. [↩]
- Ben Hilbig, the first author of this paper, helpfully pointed out that 1/6 of those who chose the concealed game would have wound up with a number that happened to match the target, and these participants would therefore not have had to lie to receive their reward. Thus, the actual percentage of liars would not be 47%, but rather 5/6 of that, which equals = 39%. This is absolutely correct if what you are capturing is “actual lying”. If you are instead capturing “willingness to lie”, then we believe that 47% is the correct number, since nobody who is not willing to lie should have chosen to play the concealed game. So overall it’s a judgment call that hinges on what you are trying to measure, actual lying or willingness to lie. [↩]
- The original authors refer to these two conditions as “C-Lab” and “C-Remote”, respectively. [↩]
- As they are careful to say in their article, the meta-analysts did not invent this measure (see Fishbacher and Föllmi-Heusi, 2013, .htm.). [↩]
- One such problem was acknowledged by the meta-analysts, who wrote, "Because participants who observed the lowest outcome were maximally tempted to lie, the estimated rate of liars is expected to be an upper bound to the 'true' rate of liars in die-roll tasks." Another problem is statistical, and occurs if meta-analysts do not allow for negative levels of dishonesty (and there are no negative values in this meta-analysis). To see why this statistical bias might emerge, imagine that you have an experiment with 64 people, and they can report 0, 1, 2, 3, or 4 tails. If everyone is honest, then on average you’d expect 4 people to observe 0 tails (.54*64 = 4). In this scenario, the probability of observing a sample that contains 3 people who report 0 tails is the same as the probability of observing a sample that contains 5 people who report 0 tails. Given the meta-analysts’ rule for computing the percentage of dishonest people, then if 3 people report 0 tails, you’d estimate 25% dishonesty (1-3/4), and if 5 people report 0 tails, then you’d estimate negative-25% dishonesty (1-5/4). If you allow for negative values, then these two estimates would cancel each other out. But if you treat the negative-25% dishonesty as 0% dishonesty, then they don’t cancel out, and you will falsely conclude that the sample contains dishonest people when it actually doesn’t. When we simulated this scenario (.R), we found that a 60-person sample that is 0% dishonest will, on average, look like a sample that is 21.7% dishonest. Allowing for negative values of dishonesty basically fixes this, although issues of rounding in small samples can do some crazy things too. (Email Joe if you want to know about the fascinating rounding thing). [↩]
- It appears that the meta-analysts miscoded two of the four results in this paper. In the original study, participants were given an envelope that contained a number from 1 to 10. Participants privately opened the envelope and reported what number they received. The higher their reported number, the more they got paid. The meta-analysts coded all four conditions as finding 100% dishonesty even though some participants did report the lowest possible outcome (1 out of 10) in two of them, and thus must have been reporting honestly. The meta-analysts’ mistake is understandable because the original article displays an arguably confusing figure (Fig. 3) that might be taken to imply that the lowest possible outcome was 0 rather than 1 (and obviously nobody reported a 0, but that was not a possible outcome.). But the original authors’ description of the methods – and their posted instructions – clearly indicates that 1 was the lowest possible outcome. [↩]
- The original authors interpret the results as indicating that nuns lie in a “disadvantageous” direction, perhaps to avoid appearing dishonest or greedy. [↩]
- We created the "% of liars" variable ourselves within the posted dataset, and confirmed that it does reproduce the authors’ result [↩]
- Instead of a difference of 52%-30% = 22%, now the difference is 52%-35% = 17%. [↩]
- The authors' analysis did include a "grouping" variable that sought to account for the fact that different findings came from the same paper, but it doesn't look like that variable did anything meaningful, since simply averaging rates of dishonesty across experimental conditions within their dataset comes extremely close to perfectly replicating their result. [↩]
