Are hidden moderators a thing? Do experiments intended to be identical lead to inexplicably different results?
Back in 2014, the "Many Labs" project (htm) reported an ambitious attempt to answer these questions. More than 30 different labs ran the same set of studies and the paper presented the results side-by-side. They did not find any evidence that hidden moderators explain failures to replicate, but did conclude that hidden moderators play a large role in studies that do replicate.
Statistically savvy observers now cite the Many Labs paper as evidence that hidden moderators, "unobserved heterogeneity", are a big deal. For example, McShane & Böckenholt (.htm) cite only the ManyLabs paper to justify this paragraph "While accounting for heterogeneity has long been regarded as important in meta-analyses of sets of studies that consist of […] [conceptual] replications, there is mounting evidence […] this is also the case [with] sets of [studies] that use identical or similar materials.” (p.1050)
Similarly, van Aert, Wicherts , and van Assen (.htm) conclude heterogeneity is something to worry about in meta-analysis by pointing out that "in 50% of the replicated psychological studies in the Many Labs Replication Project, heterogeneity was present” (p.718)
In this post I re-analyze the Many Labs data and conclude the authors substantially over-estimated the importance of hidden moderators in their data.
Aside: This post was delayed a few weeks because I couldn't reproduce some results in the Many Labs paper. See footnote for details [1].
How do you measure hidden moderators?
In meta-analysis one typically tests for the presence of hidden moderators, “unobserved heterogeneity”, by comparing how much the dependent variable jumps around across studies, to how much it jumps around within studies (This is analogous to ANOVA if that helps). Intuitively, when the differences are bigger across studies than within, we conclude that there is a hidden moderator across studies.
This was the approach taken by Many Labs [2]. Specifically, they reported a statistic called I2 for each study. I2 measures the percentage of the variation across studies that is surprising. For example, if a meta-analysis has I2=40%, then 60% of the observed differences across studies is attributed to chance, and 40% is attributed to hidden moderators.
Aside: in my opinion the I2 is kind of pointless.
We want to know if heterogeneity is substantial in absolute, not relative terms. No matter how inconsequential a hidden moderator is, as you increase sample size of the underlying studies, you will decrease the variation due to chance, and thus increase I2. Any moderator, no matter how small, can approach I2=100% with a big enough sample. To me, saying that a particular design is rich in heterogeneity because it has I2=60% is a lot like saying that a particular person is rich because she has something that is 60% gold, without specifying if the thing is her earring or her life-sized statue of Donald Trump. But I don't know very much about gold. (One could report, instead, the estimated standard deviation of effect size across studies ‘tau’ / τ). Most meta-analyses rely on I2. This is in no way a criticism of the Many Labs paper.
Criticisms of I2 along these lines have been made before, see e.g., Rucker et al (.htm) or Borenstein et al (.pdf).
I2 in Many Labs
Below is a portion of Table 3 in their paper:
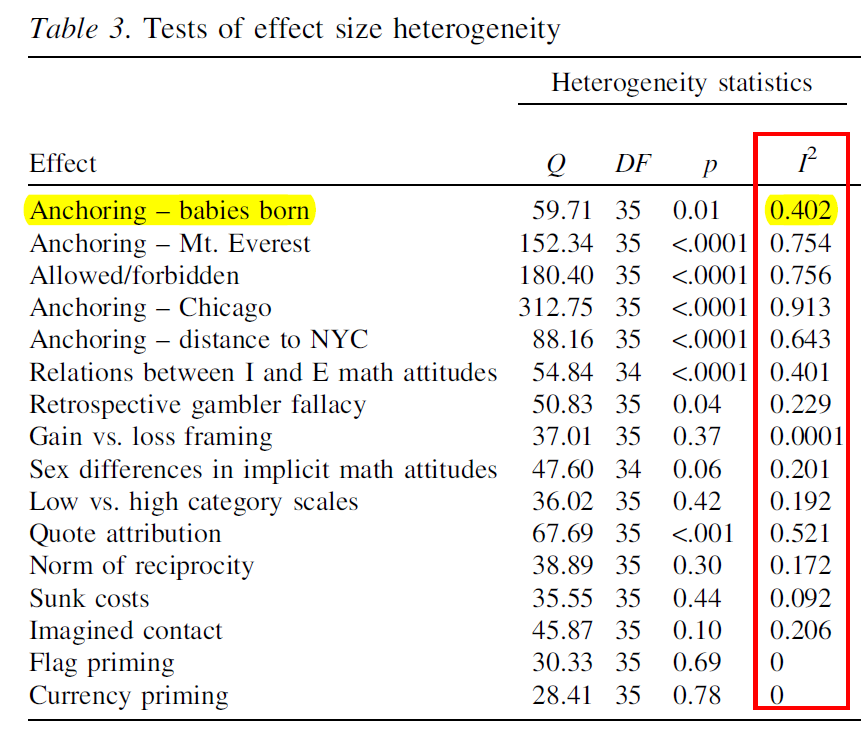
For example, the first row shows that for the first anchoring experiment, 59.8% of the variation across labs is being attributed to chance, and the remaining 40.2% to some hidden moderator.
Going down the table, we see that just over half the studies have a significant I2. Notably, four of these involve questions where participants are given an anchor and then asked to generate an open-ended numerical estimate.
For some time I have wondered if the strange distributions of responses that one tends to get with anchoring questions (bumpy, skewed, some potentially huge outliers; see histograms .png), or the data-cleaning that such responses led the Many Labs authors to take, may have biased upwards the apparent role of hidden moderators for these variables.
For this post I looked into it, and it seems like the answer is: ay, squared.
Shuffling data.
In essence, I wanted to answer the question: “If there were no hidden moderators what-so-ever in the anchoring questions in Many Labs, how likely would it be that the authors would find (false-positive) evidence for them anyway?”
To answer this question I could run simulations with made up data. But because the data were posted, there is a much better solution: run simulations with the real data. Importantly, I run the simulations “under the null,” where the data are minimally modified to ensure there is in fact no hidden moderator, and then we assess if I2 manages to realize that (it does not). This is essentially a randomization/reallocation/permutation test [3].
The posted “raw” datafile (.csv | 38Mb) has more than 6000 rows, one for each participant, across all labs. The columns have the variables for each of the 13 studies. There is also a column indicating which lab the participant is from. To run my simulations I shuffle that "lab" column. That is, I randomly sort that column, and only that column, keeping everything else in the spreadsheet intact. This creates a placebo lab column which cannot be correlated with any of the effects. With the shuffled column the effects are all, by construction, homogenous, because each observation is equally likely to originate in any “lab.” This means that variation within lab must be entirely comparable to variation across labs, and thus that the true I2 is equal to zero. When testing for heterogeneity in this shuffled dataset we are asking: are observations randomly labeled “Brian’s Lab” systematically different from those randomly labeled “Fred’s Lab”? Of course not.
This approach sounds kinda cool and kinda out-there. Indeed it is super cool, but it is as old as it gets. It is closely related to permutation tests, which was developed in the 1930s when hypothesis testing was just getting started. [4].
Results.
I shuffled the dataset, conducted a meta-analysis on each of the four anchoring questions, computed I2, and repeated this 1000 times (R Code). The first thing we can ask is how many of those meta-analyses led to a significant, false-positive, I2. How often do they wrongly conclude there is a hidden moderator?
The answer should be, for each of the 4 anchoring questions: "5%”.
But the answers are: 20%, 49%, 47% and 46%.
Yikes.
The figures below show the distributions of I2 across the simulations.
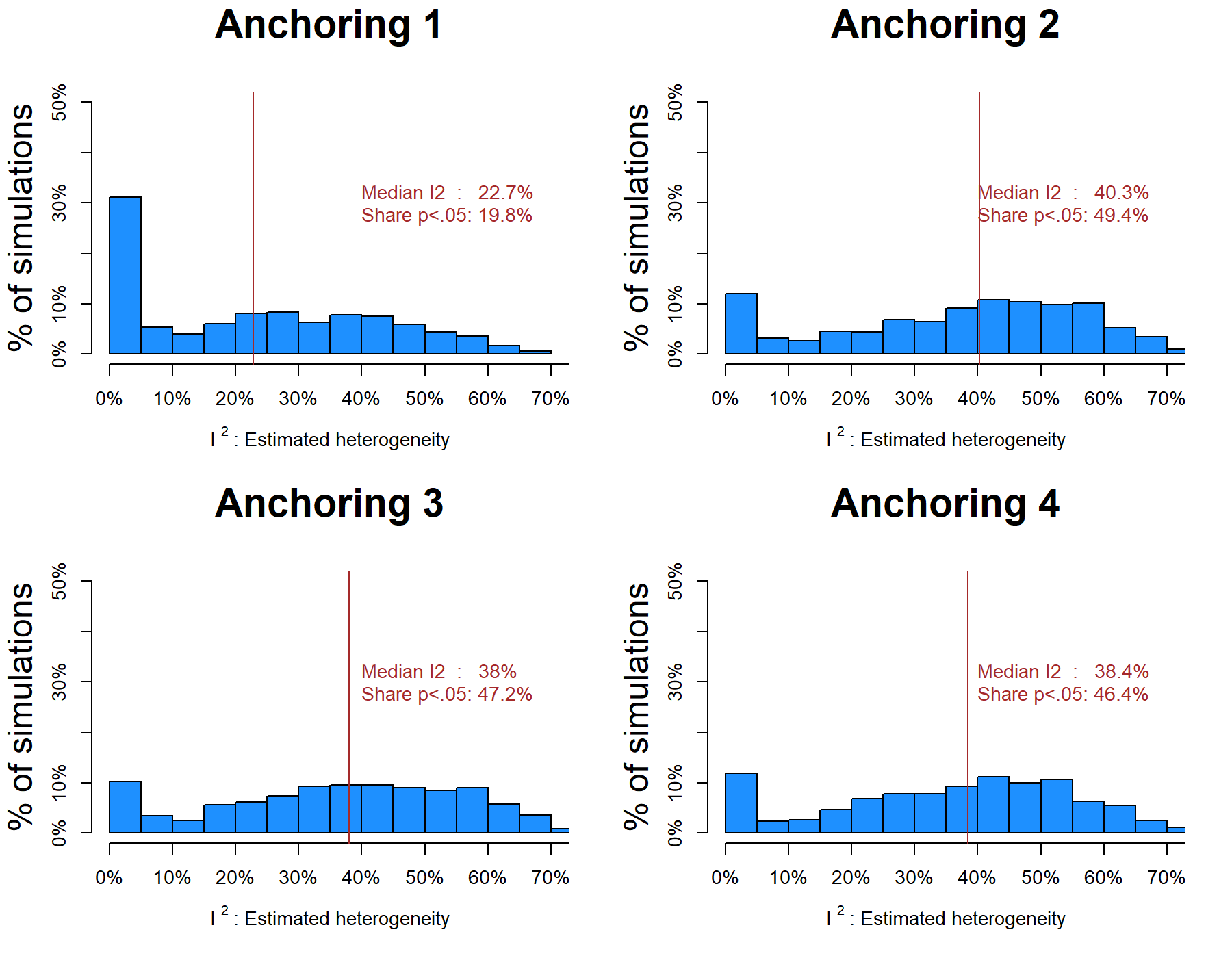 Figure 1: For the 4 anchoring questions, the hidden-moderators test Many Labs used is invalid: high false-positive rate, inflated estimates of heterogeneity (R Code).
Figure 1: For the 4 anchoring questions, the hidden-moderators test Many Labs used is invalid: high false-positive rate, inflated estimates of heterogeneity (R Code).
For example, for Anchoring 4, we see that the median estimate is that I2=38.4% of the variance is caused by hidden moderators, and 46% of the time it concludes there is statistically significant heterogeneity. Recall, the right answer is that there is zero heterogeneity, and only 5% of the time we should conclude otherwise. [5],[6],[7].
Validating the shuffle.
To reassure readers the approach I take above is valid, I submitted normally distributed data to the shuffle test. I added three columns to the Many Labs spreadsheets with made up data: In the first, the true anchoring effect was d=0 in all labs. In the second it was d=.5 in all labs. And in the third it was on average d=.5, but it varied across labs with sd(d)=.2 [8].
Recall that because the shuffle-test is done under the null, 5% of the results should be significant (false-positive), and I should get a ton of I2=0% estimates, no matter which of the three true effects are simulated.
That’s exactly what happens.
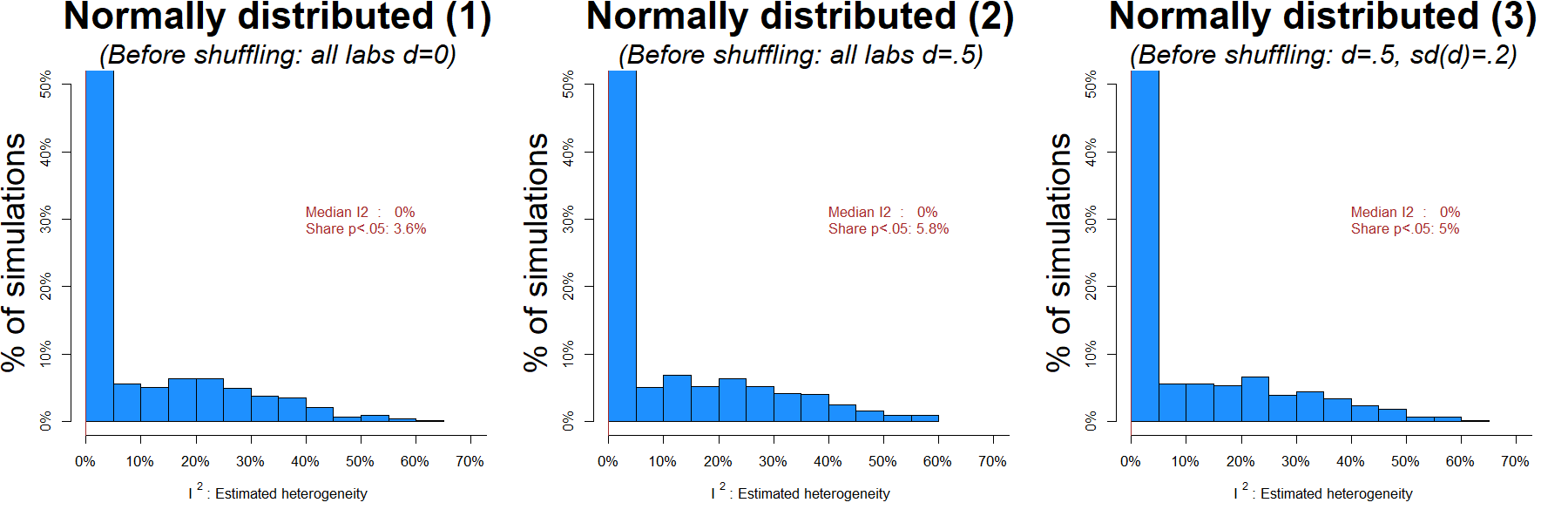 Figure 2: for normally distributed data, ~5% false-positive rate, and lots of accurate I2=0% estimates (R Code).
Figure 2: for normally distributed data, ~5% false-positive rate, and lots of accurate I2=0% estimates (R Code).
I suspect I2 can tolerate fairly non-normal data, but anchoring (or perhaps the intensive way it was 'cleaned') was too much for it. I have not looked into which specific aspect of the data, or possibly the data cleaning, disconcerts I2 [9].
Conclusions.
The authors of Many Labs saw the glass half full, concluding hidden moderators were present only in studies with big effect sizes. The statistically savvy authors of the opening paragraphs saw it mostly-empty, warning readers of hidden moderators everywhere. I see the glass mostly-full: the evidence that hidden moderators influenced large-effect anchoring studies appears to be spurious.
We should stop arguing hidden moderators are a thing based on the Many Labs paper.
Author feedback
Our policy is to share drafts of blog posts that discuss someone else’s work with them to solicit feedback (see our updated policy .htm). A constructive dialogue with several authors from Many Labs helped make progress with the reproducibility issues (see footnote 1) and improve the post more generally. They suggested I share the draft with Robbie van Aert, Jelte Wicherts and Marcel Van Assen and I did. We had an interesting discussion on the properties of randomization tests, shared some R Code back and forth, and they alerted me to the existence of the Rucker et al paper cited above.
In various email exchanges the term "hidden moderator" came up. I use the term literally: there are things we don't see (hidden) that influence the size of the effect (moderators), thus to me it is a synonym with unobserved (hidden) heterogeneity (moderators). Some authors were concerned that "hidden moderator" is a loaded term used to excuse failures to replicate. I revised the writing of the post taking that into account, hopefully making it absolutely clear that the Many Labs authors concluded that hidden moderators are not responsible for the studies that failed to replicate.
Footnotes.
- The most important problem I had was that I could not reproduce the key results in Table 3 using the posted data. As the authors explained when I shared a draft of this post, a few weeks after first asking them about this, the study names are mismatched in that table, such that the results for one study are reported in the row for a different study. A separate issue is that I tried to reproduce some extensive data cleaning performed on the anchoring questions but gave up when noticing large discrepancies between sample sizes described in the supplement and present in the data. The authors have uploaded a new supplement to the OSF where the sample sizes match the posted data files (though not the code itself that would allow reproducing the data cleaning). [↩]
- they also compared lab to online, and US vs non-US, but these are obviously observable moderators [↩]
- I originally called this "bootstrapping," many readers complained. Some were not aware modifying the data so that the null is true can also be called bootstrapping. Check out section 3 in this "Introduction to the bootstrap world" by Boos (2003) .pdf. But others were aware of it and nevertheless objected because I keep the data fixed without resampling so to them bootstrapping was misleading. Permutation is not perfect because permutation tests are associated with trying all permutations. Reallocation test is not perfect because they usually involve swapping the treatment column, not the lab column. This is a purely semantic issue, as we all know what the test I run consisted of. [↩]
- Though note that here I randomize the data to see if a statistical procedure is valid for the data, not to adjust statistical significance [↩]
- It is worth noting that the other four variables with statistically significant heterogeneity in Table 3 do not suffer from the the same unusual distributions and/or data cleaning procedures as do the four anchoring questions. But, because they are quite atypical exemplars of psychology experiments I would personally not base estimates of heterogeneity in psychology experiments in general from them. One is not an experiment, two involve items that are more culturally dependent than most psychological constructs: reactions to George Washington and an anti-democracy speech. The fourth is barely significantly heterogeneous: p=.04. But this is just my opinion [↩]
- For robustness I re-run the simulations keeping the number of observations in each condition constant within lab, the results were are just as bad. [↩]
- One could use these distributions to compute an adjusted p-value for heterogeneity; that is, compute how often we get a p-value as low as the one obtained by Many Labs, or an I2 as high as they obtained, among the shuffled datasets. But I do not do that here because such calculations should build in the data-cleaning procedures, and code for such data cleaning is not available. [↩]
- In particular, I made the effect size be proportional to the size of the name of the lab. So for the rows in the data where the lab it called “osu” the effect is d=.3, where it is “Ithaca” the effect is d=.6. As it happens, the average lab length is about 5 characters, so this works, and sd(length) is .18, which i round to .2 in the figure title. [↩]
- BTW I noted that tau makes more sense conceptually than I2 . But mathematically, for a given dataset, tau is a simple transformation of it I2 (or rather, vice versa: I2=tau2/(total variance) ) thus if one is statistically invalid, so is the other. Tau is not a more robust statistic than I2 is. [↩]
