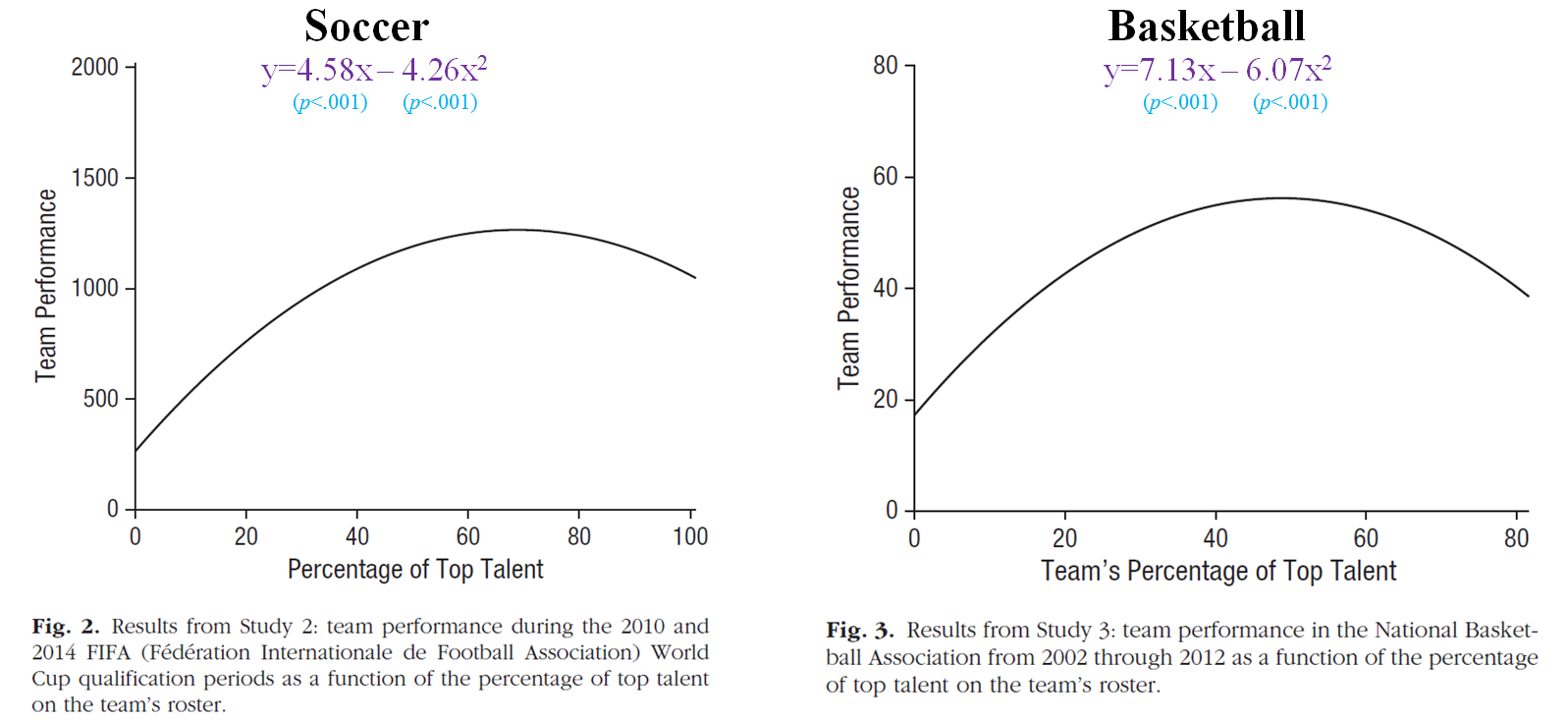
A recent Psych Science (.pdf) paper found that sports teams can perform worse when they have too much talent.
For example, in Study 3 they found that NBA teams with a higher percentage of talented players win more games, but that teams with the highest levels of talented players win fewer games.
The hypothesis is easy enough to articulate, but pause for a moment and ask yourself, “How would you test it?"
This post shows the most commonly used test is incorrect, and suggests a simple alternative.
What test would you run?
If you are like everyone we talked to over the last several weeks, you would run a quadratic regression (y=β0+β1x+β2x2), check whether β2 is significant, and whether plotting the resulting equation yields the predicted u-shape.
We browsed a dozen or so papers testing u-shapes in economics and in psychology and that is also what they did.
That’s also what the Too-Much-Talent paper did. For instance, these are the results they report for the basketball and soccer studies: a fitted inverted u-shaped curve with a statistically significant x2. [1]
Everybody is wrong
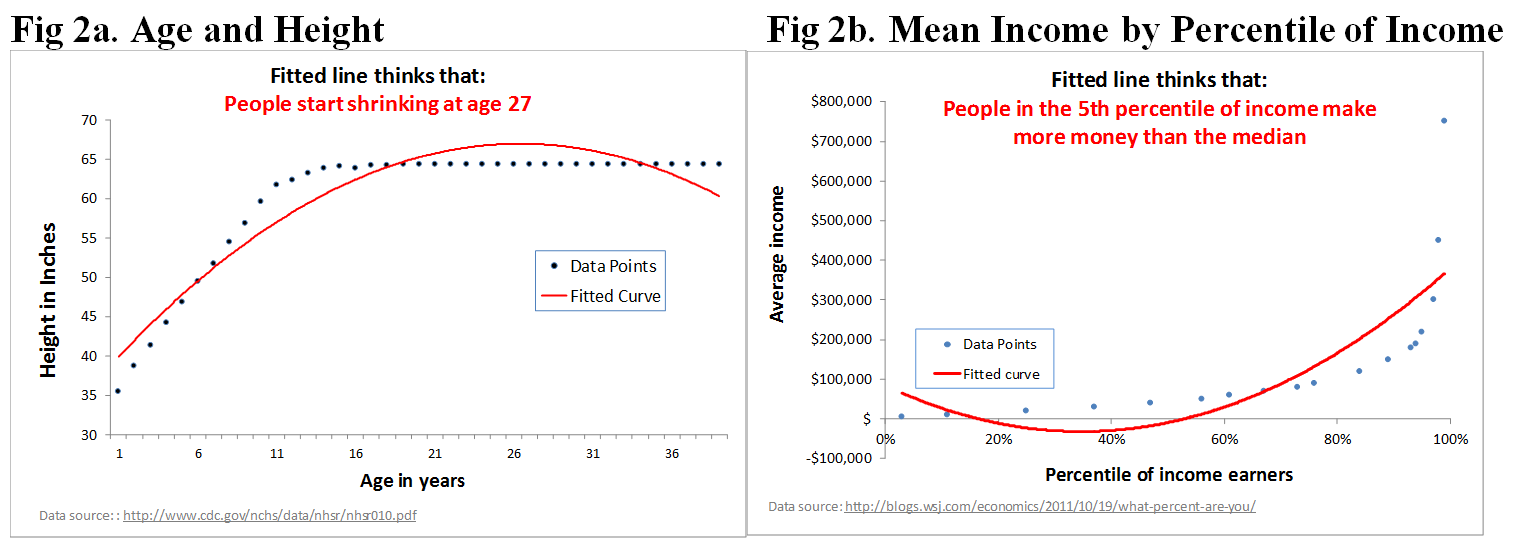
Relying on the quadratic is super problematic because it sees u-shapes everywhere, even in cases where a true u-shape is not present. For instance:
The source of the problem is that regressions work hard to get as close as possible to data (blue dots), but are indifferent to implied shapes.
A U-shaped relationship will (eventually) imply a significant quadratic, but a significant quadratic does not imply a U-shaped relationship. [2]
First, plot the raw data.
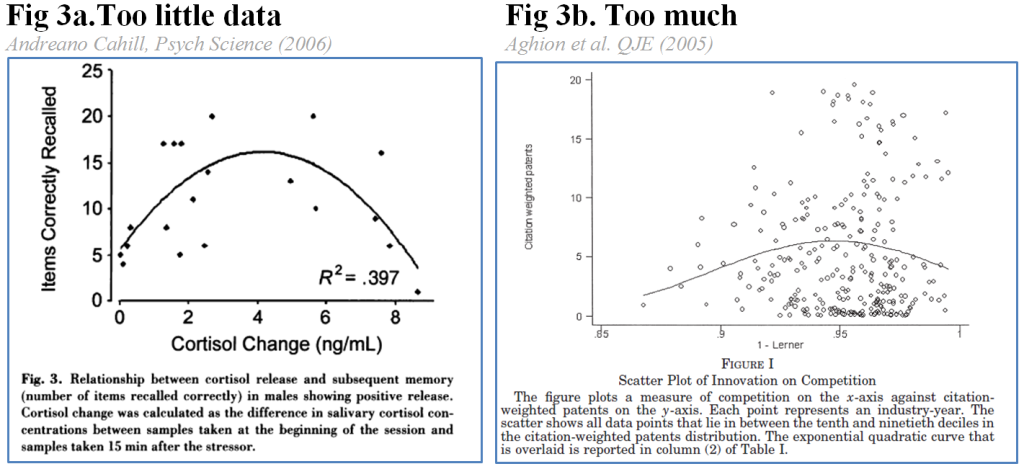
Figure 2 shows how plotting the data prevents obviously wrong answers. Plots, however, are necessary but not sufficient for good inferences. They may have too little or too much data, becoming Rorschach tests. [3]
These charts are somewhat suggestive of a u-shape, but it is hard to tell whether the quadratic is just chasing noise. As social scientists interested in summarizing a mass of data, we want to write sentences like: “As predicted, the relationship was u-shaped, p=.002.”
Those charts don’t let us do that.
A super simple solution
When testing inverted u-shapes we want to assess whether:
At first more x leads to more y, but eventually more x leads to less y.
If that’s what we want to assess, maybe that’s what we should test.Here is an easy way to do that that builds on the quadratic regression everyone is already running.
1) Run the quadratic regression
2) Find the point where the resulting u-shape maxes out.
3) Now run a linear regression up to that point, and another from that point onwards.
4) Test whether the second line is negative and significant.
More detailed step-by-step instructions (.html). [4]
One demonstration
We contacted the authors of the Too-Much-Talent paper and they proposed running the two-lines test on all three of their data sets. Aside: we think that's totally great and admirable.
They emailed us the results of those analyses, and we all agreed to include their analyses in this post.
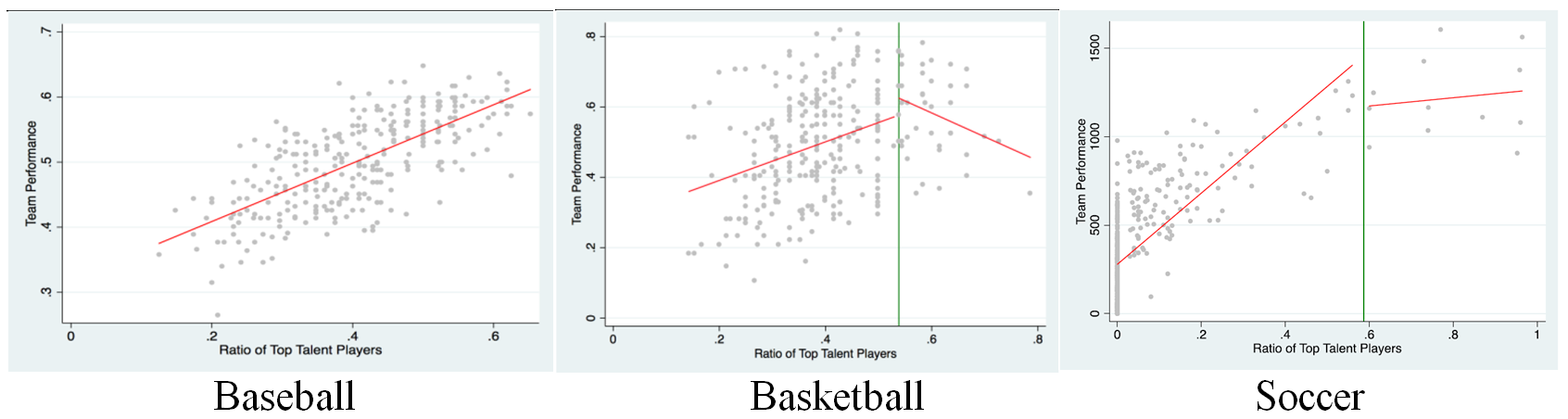
The paper had predicted and documented the lack of a u-shape for Baseball. The first figure is consistent with that result.
The paper had predicted and documented an inverted u-shape in Basketball and Soccer.The Basketball results are as predicted (first slope is positive, p<.001, second slope negative, p = .026). The Soccer results were more ambiguous (first slope is significantly positive, p<.001, but the second slope is not significant, p=.53).
The authors provided a detailed discussion of these and additional new analyses (.pdf).
We thank them for their openness, responsiveness, and valuable feedback.
Another demonstration
The most cited paper studying u-shapes we found (Aghion et al, QJE 2005, .html) examines the impact of competition on innovation. Figure 3b above is the key figure in that paper. Here it is with two lines instead (STATA code .do; raw data .zip):
The second line is significantly negatively sloped, z=-3.75, p<.0001.
If you are like us, you think the p-value from that second line adds value to the eye-ball test of the published chart, and surely to the nondiagnostic p-value from the x2 in the quadratic regression.
If you see a problem with the two lines, or know of a better solution, please email Uri and/or Leif
![]()
- Talent was operationalized in soccer as belonging to a top-25 soccer team (e.g., Manchester United) and in basketball as being top-third of the NBA in Estimated Wins Added (EWA), and results were shown to be robust to defining top-20% and top-40%. [↩]
- Lind and Mehlum (2010, .html), propose a way to formally test for the u-shape itself within a quadratic (and a few other specifications) and Miller et al (2013 .html) provide analytical techniques for calculating thresholds where effects differ from zero for quadratics models. However, these tools should only be utilized when the researcher is confident about functional form, for they can lead to mistaken inferences when the assumptions are wrong. For example, if applied to y=log(x), one would, for sufficiently dispersed x-es, incorrectly conclude the relationship has an inverted u-shape, when it obviously does not. We shared an early draft of this post with the authors of both methods papers and they provided valuable feedback already reflected in this longest of footnotes. [↩]
- One could plot fitted nonparametric functions for these, via splines or kernel regressions, but the results are quite sensitive to researcher degrees-of-freedom (e.g., bandwidth choice, # of knots) and also do not provide a formal test of a functional form [↩]
- We found one paper that implemented something similar to this approach: Ungemach et al, Psych Science, 2011, Study 2 (.html), though they identify the split point with theory rather than a quadratic regression. More generally, there are other ways to find the point where the two lines are split, and their relative performance is worth exploring. [↩]