Researchers have increasingly been using internal meta-analysis to summarize the evidence from multiple studies within the same paper. Much of the time, this involves computing the average effect size across the studies, and assessing whether that effect size is significantly different from zero.
At first glance, internal meta-analysis seems like a wonderful idea. It increases statistical power, improves precision, moves us away from focusing on single studies, incentivizes reporting non-significant results and emptying the file-drawer, etc.
When we looked closer, however, it became clear that this is the absolute worst thing the field can do. Internal meta-analysis is a remarkably effective tool for making untrue effects appear significant. It is p-hacking on steroids. So it is steroids on steroids.
We have a choice to make: to stop trusting internal meta-analysis or to burn the credibility of the field to the ground. The gory details are below, and in this paper: (SSRN).
Two Assumptions
To understand the problem, consider that the validity of internal meta-analysis rests entirely on two assumptions that are conspicuously problematic:
Assumption 1. All studies in the internal meta-analysis are completely free of p-hacking.
Assumption 2. The meta-analysis includes all valid studies.
Thinking about what it takes to meet these assumptions helps realize how implausible they are:
Assumption 1 could be met if researchers perfectly pre-registered every study included in the internal meta-analysis, and if they did not deviate from any of their pre-registrations. Assumption 2 could be met if the results of any of the studies do not influence: (1) researchers’ decisions about whether to include those studies in the meta-analysis, and (2) researchers’ decisions about whether to run additional studies to potentially include in the meta-analysis [1].
It seems unlikely that either assumption will be perfectly met, and it turns out that meeting them even a little bit imperfectly is an evidential disaster.
Violating Assumption 1: A pinch of p-hacking is very bad
Using a few common forms of p-hacking can cause the false-positive rate for a single study to increase from the nominal 5% to over 60% ("False-Positive Psychology”; SSRN). That dramatic consequence is nothing compared to what p-hacking does to internal meta-analysis.
There is an intuition that aggregation cancels out error, but that intuition fails when all components share the same bias. P-hacking may be minimal and unintentional, but it is always biased in the same direction. As a result, imperceptibly small biases in individual studies intensify when studies are statistically aggregated.
This is illustrated in the single simulation depicted in Figure 1. In this simulation, we minimally p-hacked 20 studies of an nonexistent effect (d=0). Specifically, in each study, researchers conducted two analyses instead of just one, and they reported the analysis that produced the more positive effect, even if it was not significant and even if was of the wrong sign. That's it. This level of p-hacking is so minimal that it did not even cause one of these 20 studies to be significant on its own. Nevertheless, the meta-analysis of these studies is super significant (and thus super wrong): d=.20, Z=2.81, p=.0049 [2].
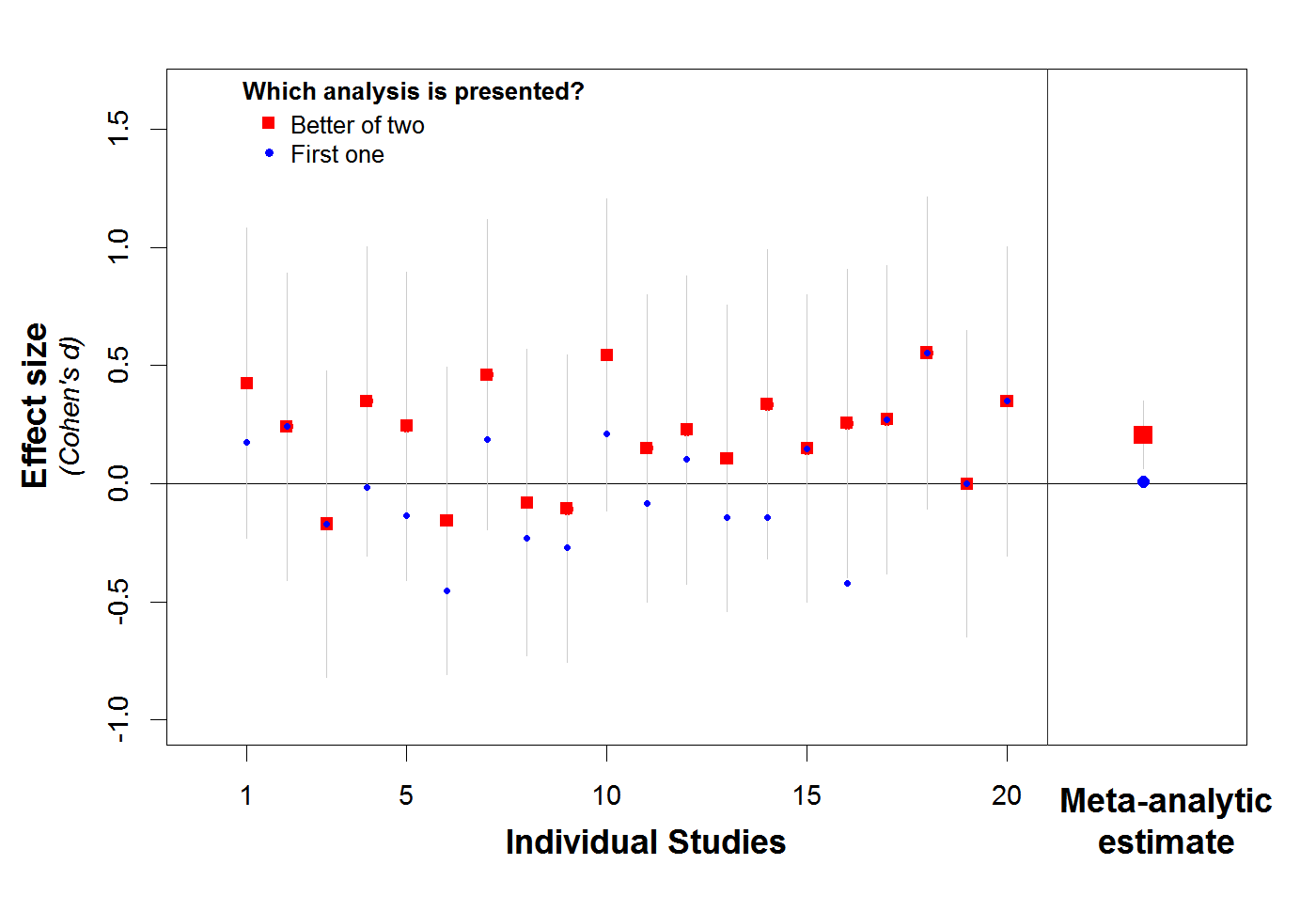Figure 1. Minimally p-hacking twenty studies of nonexistent effect leads to super significant meta-analysis.
R Code to reproduce figure.
That's one simulation. Let's see what we expect in general. The figure below shows false-positive rates for internal meta-analysis for the kind of minimal p-hacking that increases the false-positive rates of individual studies from 2.5% (for a directional hypothesis) to 6%, 7%, and 8%.
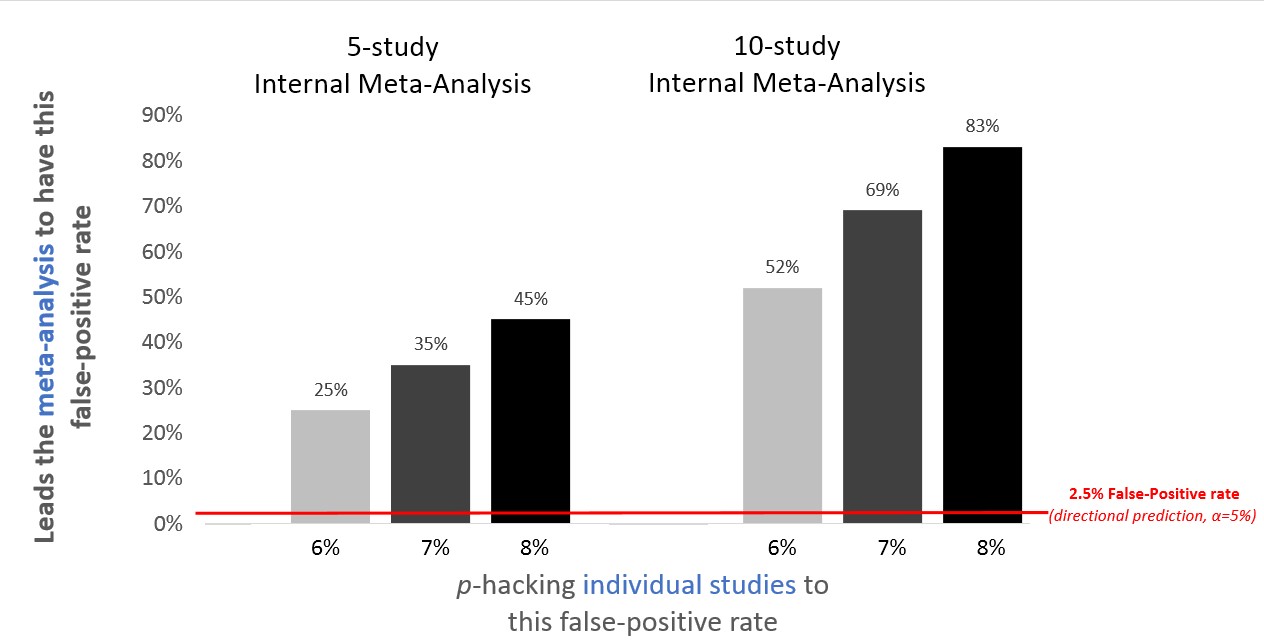Figure 2. P-hacking exerts a much larger effect on internal meta-analysis than on individual studies.
R Code to reproduce figure.
Make sure you spend time to breathe this in: If researchers barely p-hack in a way that increases their single-study false-positive rate from 2.5% to a measly 8%, the probability that their 10-study meta-analysis will yield a false-positive finding is 83%! Don’t trust internal meta-analysis.
Violating Assumption 2: Partially emptying the file-drawer makes things worse
Because internal meta-analysis leaves fewer studies in the file drawer, we may expect it to at least directionally improve things. But it turns out that partially emptying the file-drawer almost surely makes things much worse.
The problem is that researchers do not select studies at random, but are more likely to choose to include studies that are supportive of their claims. At the root of this is the fact that what counts as a valid study for a particular project is ambiguous. When deciding which studies to include in an internal meta-analysis, we must determine whether a failed study did not work because of bad design or execution (in which case it does not belong in the meta-analysis) or whether it did not work despite being competently designed and executed (in which case it belongs in the meta-analysis). Only in the utopian world of a statistics textbook do all research projects consist of several studies that unambiguously belong together. In the real world, deciding which studies belong to a project is often a messy business, and those decisions are likely to be resolved in ways that help the researchers rather than harm them. So what happens when they do that?
Imagine a one-study paper with a barely significant (p=.049) result, and the file-drawer contains two similar studies, with the same sample size, that did not “work,” a p=.20 in the right direction and a p=.20 in the wrong direction. If both of these additional studies are reported and meta-analyzed, then the overall effect would still be non-significant. But if instead the researcher only partially emptied the file drawer, including only the right-direction p=.20 in the internal meta-analysis (perhaps because the effect in the wrong direction was identified as testing a different effect, or the product of an incorrect design, etc.), then the overall p-value would drop from p=.049 to p=.021 (R Code).
Partially emptying file drawers turns weak false-positive evidence into strong false-positive evidence.
Imagine a researcher willing to file-drawer half of all attempted studies (again, because she can justify why half of them were ill-designed and thus should not be included). If she needed 5 (out of 10) individually significant studies to successfully publish her result, she would have a 1/451,398 chance of success. That's low enough not to worry about the problem; through file drawering alone we will not get many false-positive conclusions. But if instead she just needed the internal meta-analysis of the five studies to be significant, then the probability of (false-positive) success is not merely five times higher. It is 146,795 times higher. Internal meta-analysis turns a 1 in 451,398 chance of a false-positive paper into a 146,795 in 451,398 (33%) chance of a false-positive paper (R Code).
False-positive internal meta-analyses are forever
And now for the bad part.
Although correcting a single false-positive finding is often very difficult, correcting a false-positive internal meta-analysis is disproportionately harder. Indeed, we don't know how it can realistically be done.
Replicating one study won't help much
The best way to try to correct a false-positive finding is to conduct a highly powered, well-designed exact replication, and to obtain a conclusive failure to replicate. An interesting challenge with internal meta-analysis is that many (or possibly all) of the original individual studies will be non-significant. How does one “replicate” or “fail to replicate” a study that never "worked" in the first place?
Leaving that aside, how should the result from the replication of one study be analyzed? The most “meta-analytical” thing to do is to add the replication to the existing set of studies. But then even the most convincing failure-to-replicate will be unlikely to alter the meta-analytic conclusion.
Building on the simulations of the 10-study meta-analyses in Figure 2, we found that adding a replication of the same sample size leaves the meta-analytic result significant 89% of the time. Most of the time a replication won't change anything (R Code). [3]
Even replicating ALL studies is not good enough
Imagine you fail to replicate all 10 studies from Figure 2, and you re-run the meta-analyses now with 20 studies (i.e., the 10 originals and the 10 failures). If all of your replication attempts had the same sample size as those in the original studies, then 47% of false-positive internal meta-analyses would remain significant. So even if you went to the trouble of replicating every experiment, the meta-analysis would remain statistically significant almost half the time [4].
Keep in mind that all of this assumes something extremely unrealistic – that replicators could afford (or would bother) to replicate every single study in a meta-analysis and that others would judge all of those replication attempts to be of sufficient quality to count.
That is not going to happen. Once an internal meta-analysis is published, it will almost certainly never be refuted.
Conclusion
Internal meta-analysis makes false-positives easier to produce and harder to correct. Don’t do internal meta-analysis, and don’t trust any finding that is supported only by a statistically significant internal meta-analysis. Individual studies should be judged on their own merits.
Footnotes.
- This second point is made by Ueno et al (2016) .pdf [↩]
- Notice that whereas p-hacking tends to cause p-values of individual studies to be barely significant, it tends to cause p-values of meta-analyses to be VERY significant. Thus, even a very significant meta-analytic result may be a false-positive [↩]
- If it has 2.5 times the original sample size, it is still significant 81% of the time. If instead of adding the replication, one dropped the original upon failing to replicate it, essentially replacing the original study with the failure to replicate, we still find that more than 70% of false-positive internal meta-analyses survive. [↩]
- If you used 2.5 times the original sample size in all of your replication attempts, still 30% of meta-analyses would survive. [↩]