A few years ago, we developed p-curve (see p-curve.com), a statistical tool that identifies whether or not a set of statistically significant findings contains evidential value, or whether those results are solely attributable to the selective reporting of studies or analyses. It also estimates the true average power of a set of significant findings [1].
A few methods researchers have published papers stating that p-curve is biased when it is used to analyze studies with different effect sizes (i.e., studies with "heterogeneous effects"). Since effect sizes in the real world are not identical across studies, this would mean that p-curve is not very useful.
In this post, we demonstrate that p-curve performs quite well in the presence of effect size heterogeneity, and we explain why the methods researchers have stated otherwise.
Basic setup
Most of this post consists of figures like this one, which report the results of 1,000 simulated p-curve analyses (R Code).
Each analysis contains 20 studies, and each study has its own effect size, its own sample size, and because these are drawn independently, its own statistical power. In other words, the 20 studies contain heterogeneity [2].
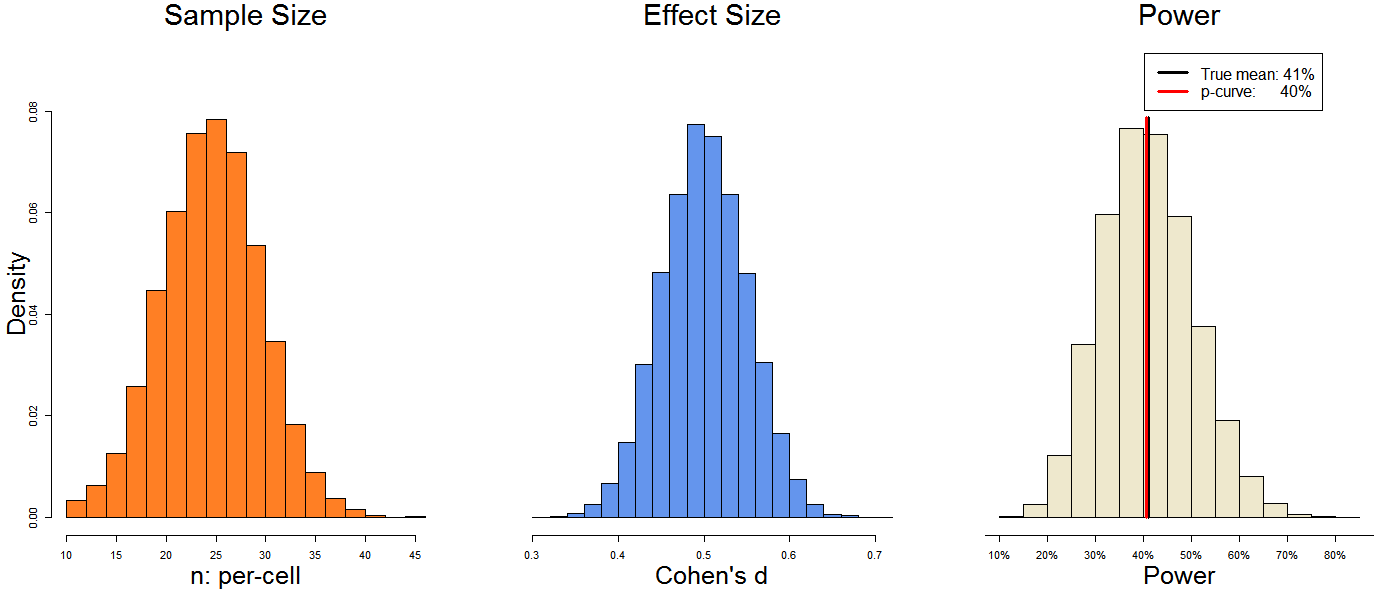
For example, to create this first figure, each analysis contained 20 studies. Each study had a sample size drawn at random from the orange histogram, a true effect size drawn at random from the blue histogram, and thus a level of statistical power drawn at random from the third histogram.
The studies’ statistical power ranged from 10% to 70%, and their average power was 41%. P-curve guessed that their average power was 40%. Not bad.
But what if…?
1) But what if there is more heterogeneity in effect size?
Let’s increase heterogeneity so that the analyzed set of studies contains effect sizes ranging from d = 0 (null) to d = 1 (very large), probably pretty close to the entire range of plausible effect sizes in psychology [3].
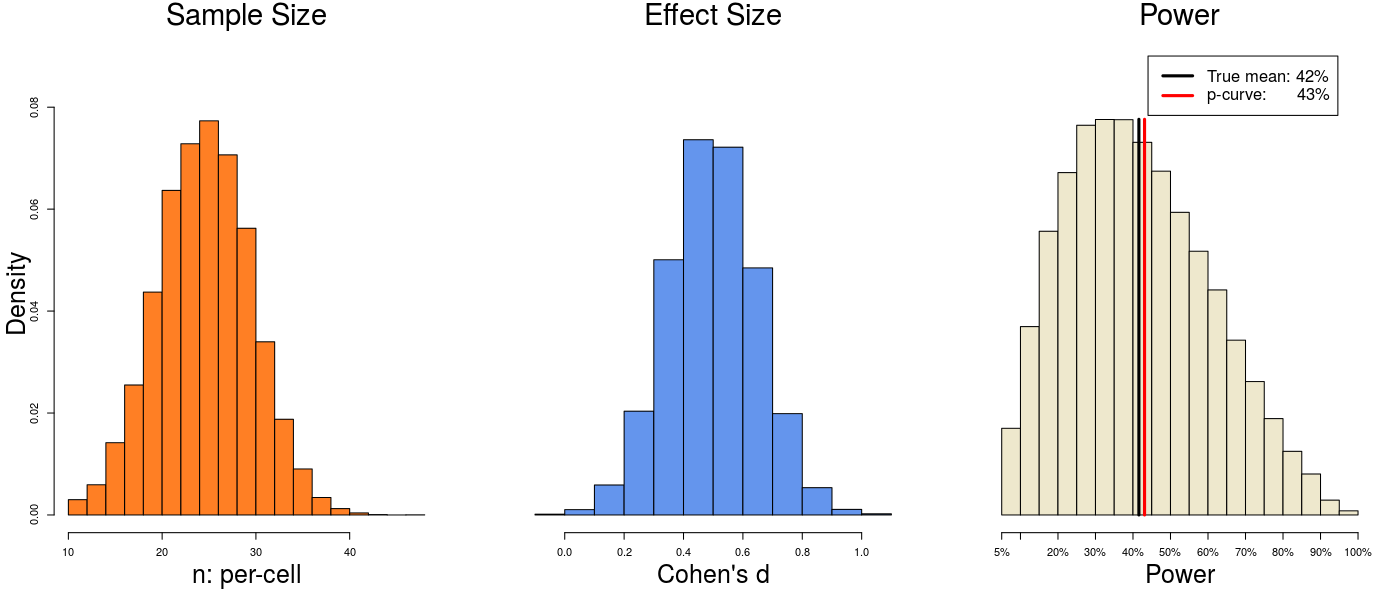The true average power is 42%. P-curve estimates 43%. Again, not bad.
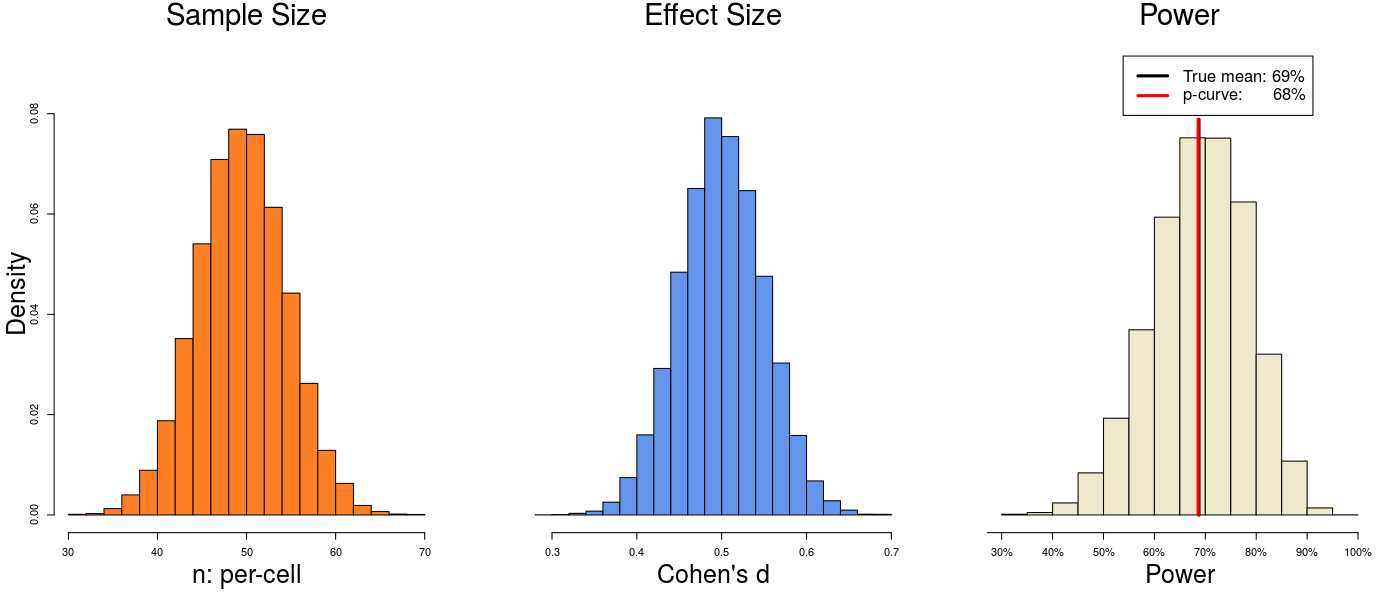
2) But what if samples are larger?
Perhaps p-curve’s success is limited to analyses of studies that are relatively underpowered. So let’s increase sample size (and therefore power) and see what happens. In this simulation, we’ve increased the average sample size from 25 per cell to 50 per cell.
The true power is 69%, and p-curve estimates 68%. This is starting to feel familiar.
3) But what if the null is true for some studies?
In real life, many p-curves will include a few truly null effects that are nevertheless significant (i.e., false-positives). Let’s now analyze 25 studies, including 5 truly null effects (d=0) that were false-positively significant.
The true power is 56%, and p-curve estimates 57%. This is continuing to feel familiar.
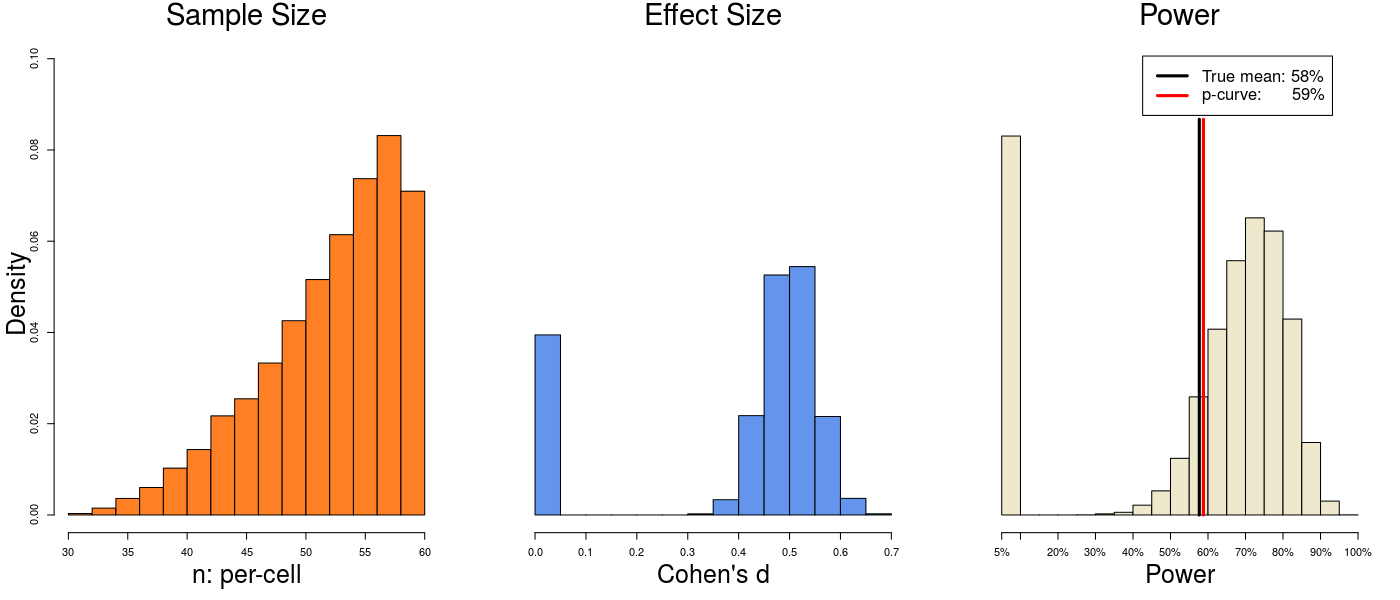
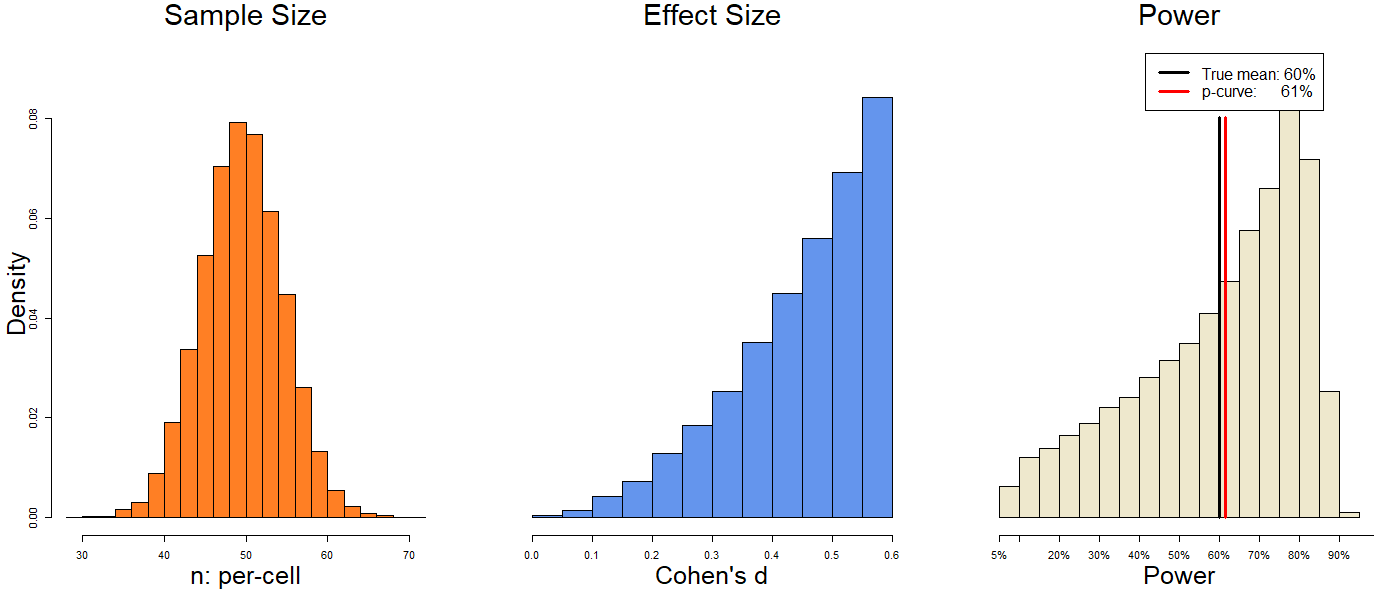
4) But what if sample size and effect size are not symmetrically distributed?
Maybe p-curve only works when sample and effect size are (unrealistically) symmetrically distributed. Let's try changing that. First we skew the sample size, then we skew the effect size:
The true powers are 58% and 60%, and p-curve estimates 59% and 61%. This is persisting in feeling familiar.
5) But what if all studies are highly powered?
Let's go back to the first simulation and increase the average sample size to 100 per cell:
The true power is 93%, and p-curve estimates 94%. It is clear that heterogeneity does not break or bias p-curve. On the contrary, p-curve does very well in the presence of heterogeneous effect sizes.
So why have others proposed that p-curve is biased in the presence of heterogeneous effects?
Reason 1: Different definitions of p-curve’s goal.
van Aert, Wicherts, & van Assen (2016, .htm) write that p-curve “overestimat[es] effect size under moderate-to-large heterogeneity” (abstract). McShane, Bockenholt, & Hansen (2016 .htm) write that p-curve “falsely assume[s] homogeneity […] produc[ing] upward[ly] biased estimates of the population average effect size.” (p.736).
We believe that the readers of those papers would be very surprised by the results we depict in the figures above. How can we reconcile our results with what these authors are claiming?
The answer is that the authors of those papers assessed how well p-curve estimated something different from what it estimates (and what we have repeatedly stated that it estimates).
They assessed how well p-curve estimated the average effect sizes of all studies that could be conducted on the topic under investigation. But p-curve informs us “only” about the studies included in p-curve [4].
Imagine that an effect is much stronger for American than for Ukrainian participants. For simplicity, let's say that all the Ukrainian studies are non-significant and thus excluded from p-curve, and that all the American studies are p<.05 and thus included in p-curve.
P-curve would recover the true average effect of the American studies. Those arguing that p-curve is biased are saying that it should recover the average effect of both the Ukrainian and American studies, even though no Ukrainian study was included in the analysis [5].
To be clear, these authors are not particularly idiosyncratic in their desire to estimate “the” overall effect. Many meta-analysts write their papers as if that’s what they wanted to estimate. However…
• We don’t think that the overall effect exists in psychology (DataColada[33]).
• We don’t think that the overall effect is of interest to psychologists (DataColada[33]).
• And we know of no tool that can credibly estimate it.
In any case, as a reader, here is your decision:
If you want to use p-curve analysis to assess the evidential value or the average power of a set of statistically significant studies, then you can do so without having to worry about heterogeneity [6].
If you instead want to assess something about a set of studies that are not analyzed by p-curve, including studies never observed or even conducted, do not run p-curve analysis. And good luck with that.
Reason 2: Outliers vs heterogeneity
Uli Schimmack, in a working paper (.pdf), reports that p-curve overestimates statistical power in the presence of heterogeneity. Just like us, and unlike the previously referenced authors, he is looking only at the studies included in p-curve. Why do we get different results?
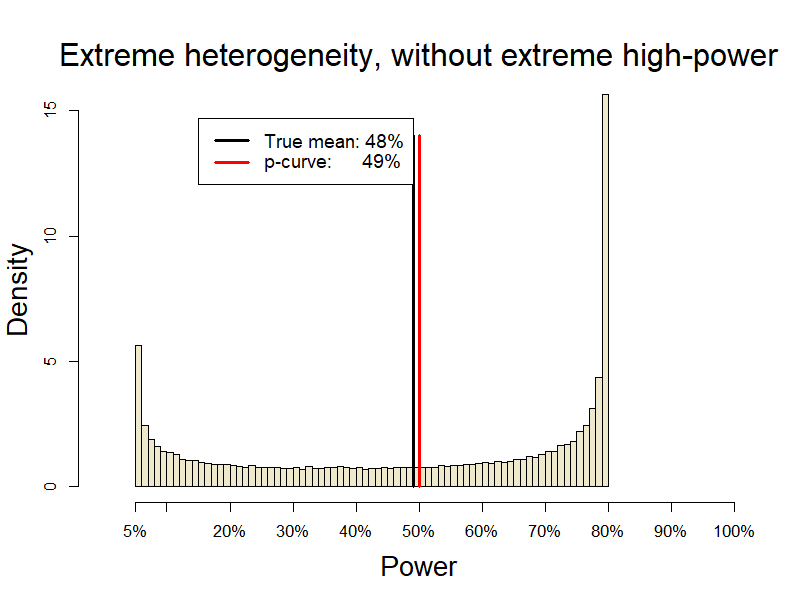
It will be useful to look at a concrete simulation he has proposed, one in which p-curve does indeed do poorly (R Code):
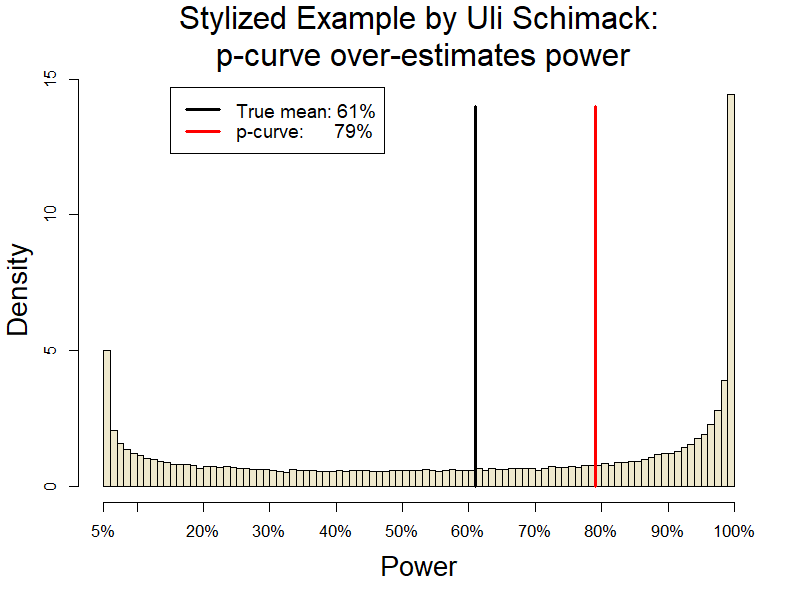
Although p-curve overestimates power in this scenario, the culprit is not heterogeneity, but rather the presence of outliers, namely several extremely highly powered studies. To see this let's look at similarly heterogeneous studies, but ones in which the maximum power is 80% instead of 100%.
In a nutshell the overestimation with outliers occurs because power is a bounded variable but p-curve estimates it based on an unbounded latent variable (the noncentrality parameter). It's worth keeping in mind that a single outlier does not greatly bias p-curve. For example, if 20 studies are powered on average to 50%, adding one study powered to 95% increases true average power to 52%, p-curve's estimate to just 54%.
This problem that Uli has identified is worth taking into account and perhaps p-curve can be modified to prevent such bias [7]. But it is worth keeping in mind that this situation should be rare, as few literatures contain both (1) a substantial number of studies powered over 90% and (2) a substantial number of under-powered studies. Moreover, this is somewhat inconsequential mistake. All it means is that p-curve will exaggerate how strong a truly (and obviously) strong literature actually is.
In Summary
• P-curve is not biased by heterogeneity.
• It is biased upwards in the presence of both (1) low powered studies, and (2) a large share of extremely highly powered studies.
• P-curve tells us about the study designs it includes, not the study designs it excludes.
Author feedback.
Our policy (.htm) is to share, prior to publication, drafts of posts with original authors whose work we discuss, asking them to identify anything that is unfair, inaccurate, misleading, snarky, or poorly worded.
We contacted all 7 authors of the three methods papers discussed above. Uli Schimmack declined to comment. Karsten Hansen and Blake McShane provided suggestions that led us to more precisely describe their analyses and to describe more detailed analyses in Footnote 5. Though our exchange with Karsten and Blake started and ended with, in their words, "fundamental disagreements about the nature of evaluating the statistical properties of an estimator,” the dialogue was friendly and constructive. We are very grateful to them, both for the feedback and for the tone of the discussion. (Interestingly, we disagree with them about the nature of our disagreement: we don't think we disagree about how to examine the statistical properties of an estimator, but rather, about how to effectively communicate methods issues to a general audience). Marcel van Assen, Robbie van Aert, and Jelte Wicherts disagreed with our belief that readers of their paper would be surprised by how well p-curve recovers average power in the presence of heterogeneity (as they think their paper explains this as well). Specifically, like us, they think p-curve performs well when making inferences about studies included in p-curve, but, unlike us, they think that readers of their paper would realize this. They are not persuaded by our arguments that the population effect size does not exist and is not of interest to psychologists, and they are troubled by the fact that p-curve does not recover this effect. They also proposed that an important share of studies may indeed have power near 100% (citing this paper: .htm). We are very grateful to them for their feedback and collegiality as well.
Footnotes.
- P-curve can also be used to estimate average effect size rather than power (and, as Blake McShane and Karsten Hansen pointed out to us, when used in this fashion p-curve is virtually equivalent to the maximum likelihood procedure proposed by Hedges in 1984 (.htm) ). Here we focus on power rather than effect size because we don't think "average effect size" is meaningful or of interest when aggregating across psychology experiments with different designs (see Colada[33]). Moreover, whereas power calculations only require that one knows the results of the test statistic of interest (e.g., F(1,230)=5.23), effect size calculations require one to also know how the study was defined, a fact that renders effect size estimations much more prone to human error (see page 676 of our article on p-curve and effect size estimation (.htm) ). In any case, the point that we make in this post applies at least as strongly to an analysis of effect size as it does to an analysis of power: p-curve correctly recovers the true average effect size of the studies that it analyses, even when those studies contain different (i.e., heterogeneous) effect sizes. See Figure 2c in our article on p-curve and effect size estimation (.htm) and Supplement 2 of that same paper (.pdf) [↩]
- In real life, researchers are probably more likely to collect larger samples when studying smaller effects (see Colada[58]). This would necessarily reduce heterogeneity in power across studies [↩]
- To do this, we changed the blue histogram from d~N(.5,.05) to d~N(.5,.15). [↩]
- We have always been transparent about this. For instance, when we described how to use p-curve for effect size estimation (.htm) we wrote, "Here is an intuitive way to think of p-curve’s estimate: It is the average effect size one expects to get if one were to rerun all studies included in p-curve." (p.667). [↩]
- For a more quantitative example check out Supplement 2 (.pdf) of our p-curve and effect size paper. In the middle panel of Figure S2, we consider a scenario in which a research attempts to run an equal number of studies (with n = 20 per cell) testing either an effect size of d = .2 or an effect size of d = .6. Because it necessarily easier to get significance when the effect size is larger than when the effect size is smaller, the share of significant d = .6 studies will necessarily be greater than the share of significant d = .2 studies, and thus p-curve will include more d = .6 studies that d = .2 studies. Because the d = .6 studies will be over-represented among all significant studies, the true average efefct of the significant studies will be d = .53 rather than d=.4. P-curve correctly recovers this value (.53), but it is biased upwards if we expect it to guess d=.4. For an even more quantitative example, imagine the true average effect is d = .5 with a standard deviation of .2. If we study this with many n=20 studies, the average observed significant effect will be d=.91, but the true average effect of those studies is d = .61, which is the number that p-curve would recover. It would not recover the true mean of the population (d = .5) but rather the true mean of the studies that were statistically significant (d = .61). In simulations, the true mean is known and this might look like a bias. In real life, the true mean is, well, meaningless, as it depends on arbitrary definitions of what constitutes the true population of all possible studies; R Code) [↩]
- Again, for both practical and conceptual reasons, we would not advise you to estimate the average effect size, regardless of whether you use p-curve or any other tool. But this has nothing to do with the supposed inability of p-curve to handle heterogeneity. See footnote 1. [↩]
- Uli has proposed using z-curve, a tool he developed, instead of p-curve. While z-curve does not seem to be biased in scenarios with many studies with extreme high-power, it performs worse than p-curve in almost all other scenarios. For example, in the examples depicted graphically in this post, z-curve’s expected estimates are about 4 times further from the truth than are p-curve's. [↩]