In a recent critique, Bruns and Ioannidis (PlosONE 2016 .htm) proposed that p-curve makes mistakes when analyzing studies that have collected field/observational data. They write that in such cases:
p-curves based on true effects and p‑curves based on null-effects with p-hacking cannot be reliably distinguished” (abstract).
In this post we show, with examples involving sex, guns, and the supreme court, that the statement is incorrect. P-curve does reliably distinguish between null effects and non-null effects. The observational nature of the data isn’t relevant.
The erroneous conclusion seems to arise from their imprecise use of terminology. Bruns & Ioannidis treat a false-positive finding and a confounded finding as the same thing. But they are different things. The distinction is as straightforward as it is important.
Confound vs False-positive.
We present examples to clarify the distinction, but first let's speak conceptually.
A Confounded effect of X on Y is real, but the association arises because another (omitted) variable causes both X and Y. A new study of X on Y is expected to find that association again.
A False-positive effect of X on Y, in contrast, is not real. The apparent association between X and Y is entirely the result of sampling error. A new study of X on Y is not expected to find an association again.
Confounded effects are real and replicable, while false-positive effects are neither. Those are big differences, but Bruns & Ioannidis conflate them. For instance, they write:
the estimated effect size may be different from zero due to an omitted-variable bias rather than due to a true effect. (p. 3; emphasis added).
Omitted-variable bias does not make a relationship untrue; it makes it un-causal.
This is not just semantics, nor merely a discussion of "what do you mean by a true effect?"
We can learn something from examining replicable effects further (e.g., learn if there is a confound and what it is; confounds are sometimes interesting). We cannot learn something from examining non-replicable effects further.
This critical distinction between replicable and non-replicable effects can be informed by p-curve. Replicable results, whether causal or not, lead to right-skewed p-curves. False-positive, non-replicable effects lead to flat or left-skewed p-curves.
Causality
P-curve’s inability to distinguish causal vs. confounded relationships is no more of a shortcoming than is its inability to fold laundry or file income tax returns. Identifying causal relationships is not something we can reasonably expect any statistical test to do [1].
When researchers try to assess causality through techniques such as instrumental variables, regression discontinuity, or randomized field experiments, they do so via superior designs, not via superior statistical tests. The Z, t, and F tests reported in papers that credibly establish causality are the same tests as those reported in papers that do not.
Correlation is not causation. Confusing the two is human error, not tool error.
To make things concrete we provide two examples. Both use General Social Survey (GSS) data, which is, of course, observational data.
Example 1. Shotguns and female partners (Confound)
With the full GSS, we identified the following confounded association: Shotgun owners report having had 1.9 more female sexual partners, on average, than do non-owners, t(14824)=10.58, p<.0001. The omitted variable is gender.
33% of Male respondents report owning a shotgun, whereas, um, 'only' 19% of Women do.
Males, relative to females, also report having had a greater number of sexual encounters with females (means of 9.82 vs 0.21)
Moreover, controlling for gender, the effect goes away (t(14823)=.68, p=.496) [2].
So the relationship is confounded. It is real but not causal. Let's see what p-curve thinks of it. We use data from 1994 as the focal study, and create a p-curve using data from previous years (1989-1993) following a procedure similar to Bruns and Ioannidis (2016) [3]. Panel A in Figure 1 shows the resulting right-skewed p-curve. It suggests the finding should replicate in subsequent years. Panel B shows that it does.
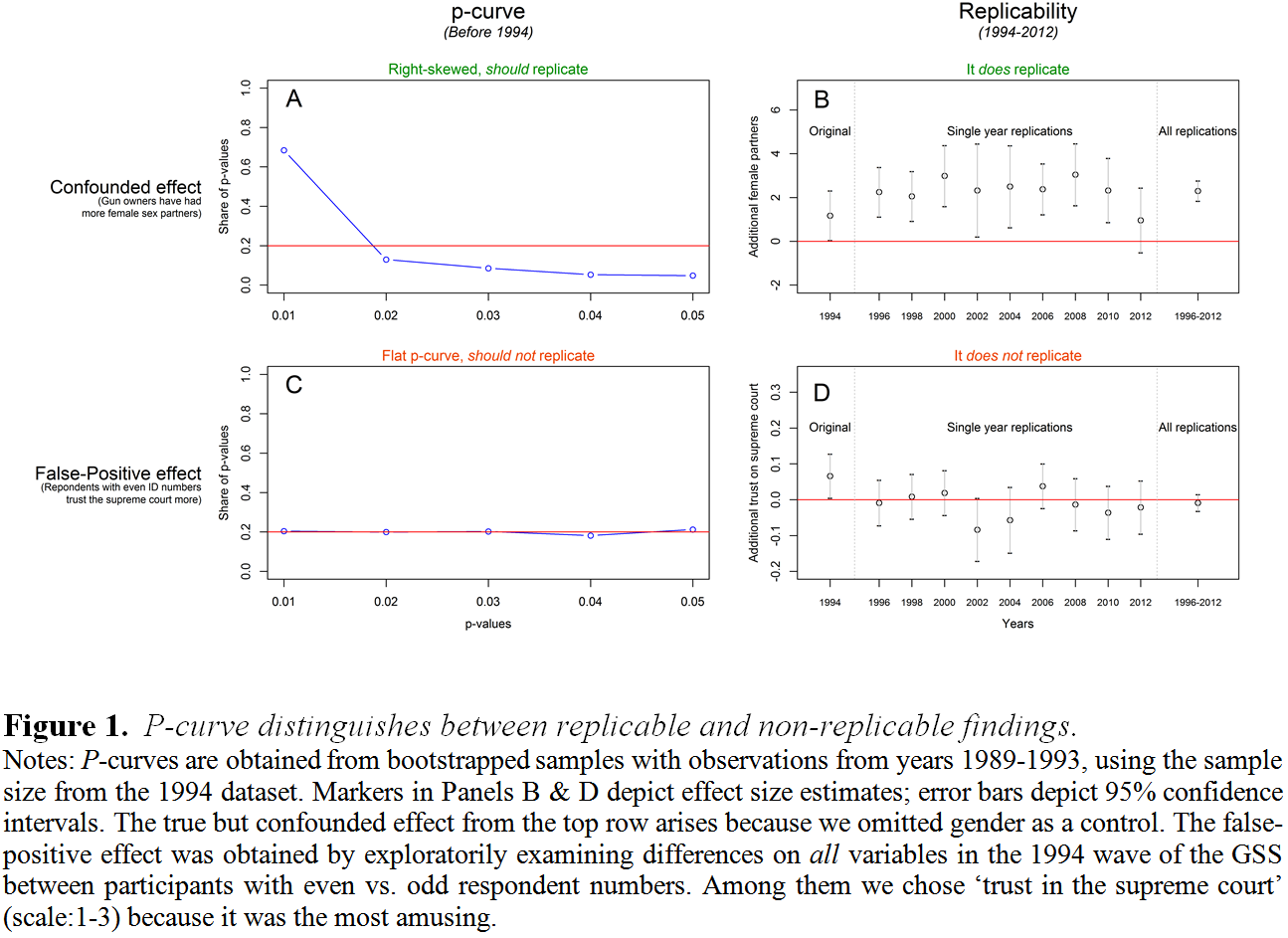R Code to reproduce this figure: https://osf.io/wn7ju/
Example 2. Random numbers and the Supreme Court (false-positive)
With observational data it’s hard to identify exactly zero effects because there is always the risk of omitted variables, selection bias, long and difficult-to-understand causal chains, etc.
To create a definitely false-positive finding we started with a predictor that could not possibly be expected to truly correlate with any variable: whether the random respondent ID was odd vs. even.
We then p-hacked an effect by running t-tests on every other variable in the 1994 GSS dataset for odd vs. even participants, arriving at 36 false-positive ps<.05. For its amusement value, we focused on the question asking participants how much confidence they have in the U.S. Supreme Court (1: a great deal, 2: only some, 3: hardly any).
Panel C in Figure 1 shows that, following the same procedure as for the previous example, the p-curve for this finding is flat, suggesting that the finding would not replicate in subsequent years. Panel D shows that it does not. Figure 1 demonstrates how p-curve successfully distinguishes between statistically significant studies that are vs. are not expected to replicate.
Punchline: p-curve can distinguish replicable from non-replicable findings. To distinguish correlational from causal findings, call an expert.
Note: this is a blog-adapted version of a formal reply we wrote and submitted to PlosONE, but since 2 months have passed and they have not sent it out to reviewers yet, we decided to Colada it and hope someday PlosONE generously decides to send our paper out for review.
Author feedback.
Our policy is to contact authors whose work we discuss to request feedback and give an opportunity to respond within our original post. We contacted Stephan Bruns and John Ioannidis. They didn't object to our distinction between confounded and false-positive findings, but propose that "the ability of 'experts' to identify confounding is close to non-existent." See their full 3-page response (.pdf).
Footnotes.
- For what is worth, we have acknowledged this in prior work. For example, in Simonsohn, Nelson, and Simmons (2014, p. 535) we wrote, “Just as an individual finding may be statistically significant even if the theory it tests is incorrect— because the study is flawed (e.g., due to confounds, demand effects, etc.)—a set of studies investigating incorrect theories may nevertheless contain evidential value precisely because that set of studies is flawed” (emphasis added). [↩]
- We are not claiming, of course, that the residual effect is exactly zero. That's untestable. [↩]
- In particular, we generated random subsamples (of the size of the 1994 sample), re-ran the regression predicting number of female sexual partners with the shotgun ownership dummy, and constructed a p-curve for the subset of statistically significant results that were obtained. This procedure is not really necessary. Once we know the effect size and sample size we know the non-centrality parameter of the distribution for the test-statistic and can compute expected p-curves without simulations (see Supplement 1 in Simonsohn et al., 2014), but we did our best to follow the procedures by Bruns and Ioannidis. [↩]