Back in May 2012, we were interested in the question of how many participants a typical between-subjects psychology study needs to have an 80% chance to detect a true effect. To answer this, you need to know the effect size for a typical study, which you can’t know from examining the published literature because it severely overestimates them (.html1; html2; .html3).
To begin to answer this question, we set out to estimate some effects we expected to be very large, such as “people who like eggs report eating egg salad more often than people who don't like eggs.” We did this assuming that the typical psychology study is probably investigating an effect no bigger than this. Thus, we reasoned that the sample size needed to detect this effect is probably smaller than the sample size psychologists typically need to detect the effects that they study.
We investigated a bunch of these “obvious” effects in a survey on amazon.com’s Mechanical Turk (N=697). The results are bad news for those who think 10-40 participants per cell is an adequate sample.
Turns out you need 47 participants per cell to detect that people who like eggs eat egg salad more often than those who dislike eggs. The finding that smokers think that smoking is less likely to kill someone requires 149 participants per cell. The irrefutable takeaway is that, to be appropriately powered, our samples must be a lot larger than they have been in the past, a point that we’ve made in a talk on “Life After P-Hacking” (slides).
Of course, “irrefutable” takeaways inevitably invite attempts at refutation. One thoughtful attempt is the suggestion that the effect sizes we observed were so small because we used MTurk participants, who are supposedly inattentive and whose responses are supposedly noisy. The claim is that these effect sizes would be much larger if we ran this survey in the Lab, and so samples in the Lab don’t need to be nearly as big as our MTurk investigation suggests.
MTurk vs. The Lab
Not having yet read some excellent papers investigating MTurk’s data quality (the quality is good; .pdf1pdf .html2; .pdf3), I ran nearly the exact same survey in Wharton’s Behavioral Lab (N=192), where mostly undergraduate participants are paid $10 to do an hour’s worth of experiments.
I then compared the effect sizes between MTurk and the Lab (materials .pdf; data .xls). [1] Turns out…
…MTurk and the Lab did not differ much. You need big samples in both.
Six of the 10 the effects we studied were directionally smaller in the Lab sample: [2]
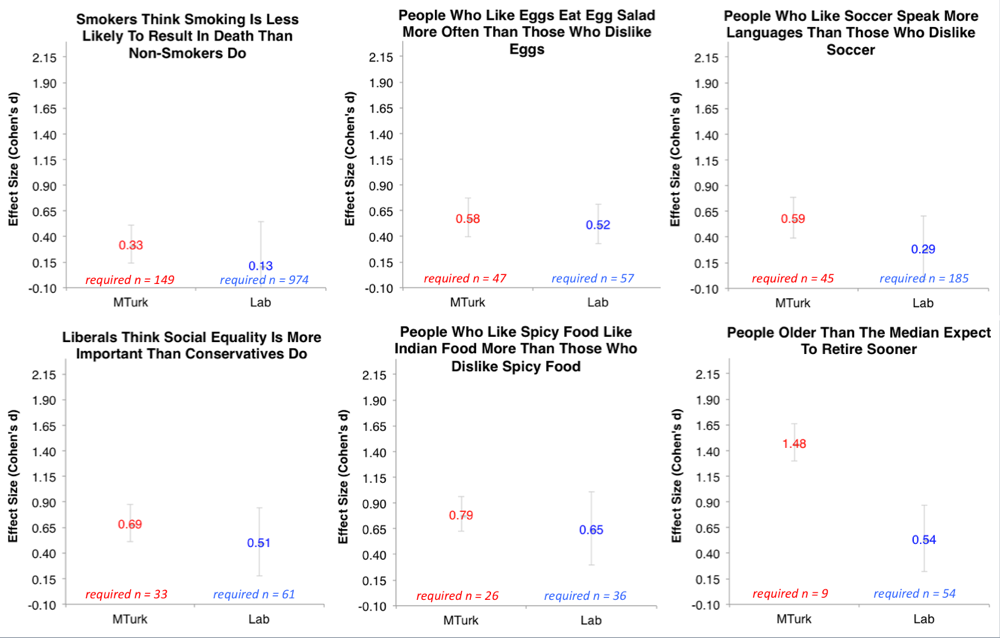
No matter what, you need ~50 per cell to detect that egg-likers eat egg salad more often. The one effect resembling something psychologists might actually care about – smokers think that smoking is less likely to kill someone – was actually quite a bit smaller in the Lab sample than in the MTurk sample: to detect this effect in our Lab would actually require many more participants than on MTurk (974 vs. 149 per cell).
Four out of 10 effect sizes were directionally larger in the Lab, three of them involving gender differences:
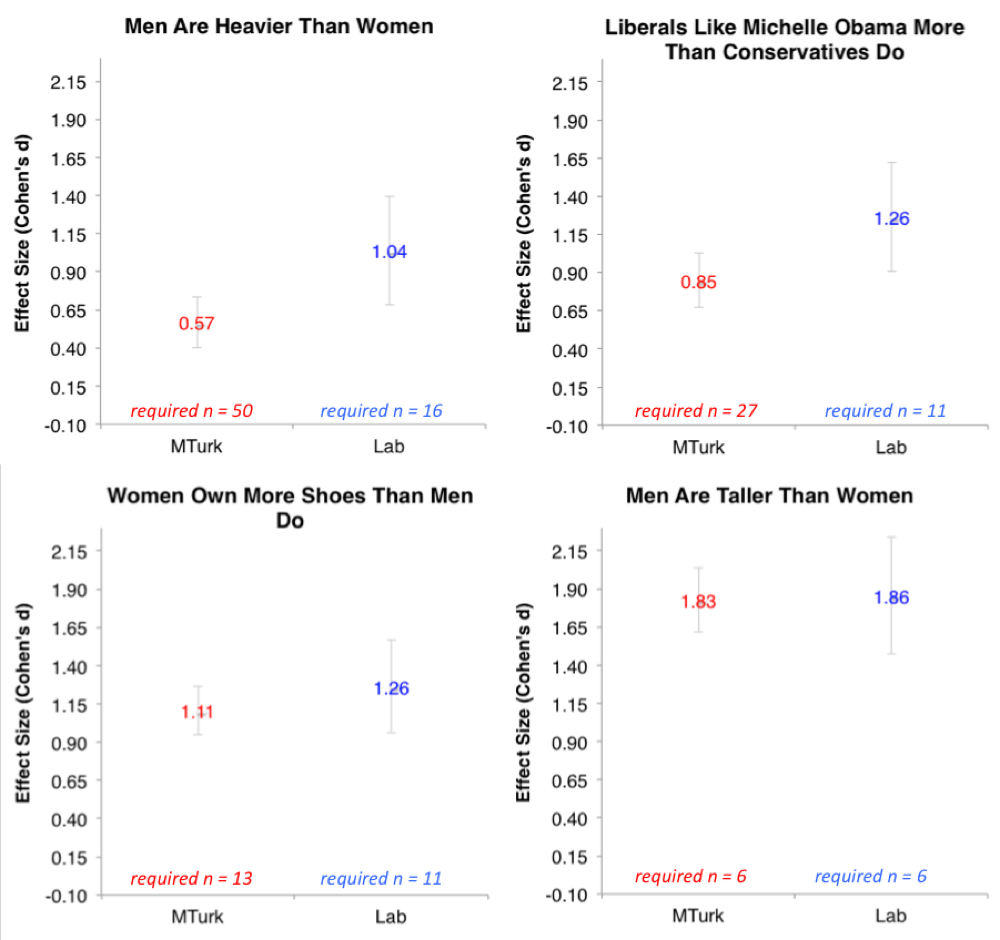
So across the 10 items, some of the effects were bigger in the Lab sample and some were bigger in the MTurk sample.
Most of the effect sizes were very similar, and any differences that emerged almost certainly reflect differences in population rather than data quality. For example, gender differences in weight were bigger in the Lab because few overweight individuals visit our lab. The MTurk sample, by being more representative, had a larger variance and thus a smaller effect size than did the Lab sample [3].
Conclusion
MTurk is not perfect. As with anything, there are limitations, especially the problem of nonnaïvete (.html), and since it is a tool that so many of us use, we should continue to monitor the quality of the data that it produces. With that said, the claim that MTurk studies require larger samples is based on intuitions unsupported by evidence.
So whether we are running our studies on MTurk or in the Lab, the irrefutable fact remains:
We need big samples. And 50 per cell is not big.
- To eliminate outliers, I trimmed open-ended responses below the 5th and above the 95th percentiles. This increases effect size estimates. If you don't do this, you need even more participants for the open-ended items than the figures below suggest. [↩]
- For space considerations, here I report only the 10 of 12 effects that were significant in at least one of the samples; the .xls file shows the full results. The error bars are 95% confidence intervals. [↩]
- MTurk’s gender on weight effect size estimate more closely aligns with other nationally representative investigations (.pdf) [↩]
