A number of authors have recently proposed that (i) psychological research is highly unpredictable, with identical studies obtaining surprisingly different results, (ii) the presence of heterogeneity decreases the replicability of psychological findings. In this post we provide evidence that contradicts both propositions.
Consider these quotes:
"heterogeneity persists, and to a reasonable degree, even in […] Many Labs projects […] where rigid, vetted protocols with identical study materials are followed […] heterogeneity […] cannot be avoided in psychological research—even if every effort is taken to eliminate it."
McShane, Tackett, Böckenholt, and Gelman (American Statistician 2019 .htm)
“Heterogeneity […] makes it unlikely that the typical psychological study can be closely replicated”
Stanley, Carter, and Doucouliagos (Psychological Bulletin 2018 .htm)
"Repeated investigations of the same phenomenon [get] effect sizes that vary more than one would expect […] even in exact replication studies. […] In the presence of heterogeneity, […] even large N studies may find a result in the opposite direction from the original study. This makes us question the wisdom of placing a great deal of faith in a single replication study"
Judd and Kenny (Psychological Methods 2019 .htm)
This post is not an evaluation of the totality of these three papers, but rather a specific evaluation of the claims in the quoted text. In the case of the paper by Judd and Kenny, the claims quoted above are secondary, used to motivate the remainder of their paper (e.g., in the opening lines of their abstract).
Heterogeneity: observable vs not.
To begin, it is important to distinguish between two types of heterogeneity:
- Observable heterogeneity: When studies that look different obtain surprisingly different results.
- Unobservable heterogeneity: When studies that look identical obtain surprisingly different results.
Note: by "surprisingly" we mean "beyond what's expected by sampling error alone."
In what follows, we do two things.
First, we report new data demonstrating that observable heterogeneity across studies does not imply low replicability. Second, we revisit the data behind the quotes above, finding there is no support for the conclusions that unobservable heterogeneity is rampant, or even present, in studies with identical designs (i.e., the Many Labs studies).
(You can reproduce all of the results in this post: links to materials, data, and code: .pdf.)
New Data: Maluma and Takiti Walk Into a Bar (Chart).
Our first demonstration is based on a classic Gestalt psychology study, first reported by Wolfgang Köhler in 1929. He presented participants with two shapes, one with jagged edges and one with rounded "edges," as in the gray figures above. He then asked them which one should be called “Maluma” and which one should be called “Takiti.” The vast majority of participants said that the rounded shape must be “Maluma.” This effect was gigantic in the 1920s, and it is still gigantic today. It replicates nicely in class [1] [2].
We conducted 50 variations of this "Maluma-Takiti" paradigm, but instead of using the words “Maluma-Takiti,” we used a Dutch boy name paired with a Dutch girl name. Specifically, we got a list of the 50 most popular baby names in the Netherlands in 2016 (source: .htm) and we paired the first name of the girl’s list with the first name on the boy’s list, and then the second name on the girl’s list with the second name on the boy’s list, and then….you get the idea. For example, our first study pitted the most popular boy name, Daan, against the most popular girl name, Anna, as follows [3].
We ran the first wave of 50 studies in June of 2017. In total, we asked 508 U.S. MTurk participants to complete 10 studies each during a single session, and so there were about 100 observations per study [4]. We expected girl names to be assigned to the rounded shape more often than the boy names, but that this effect would vary substantially across name pairs. The studies came out as expected.
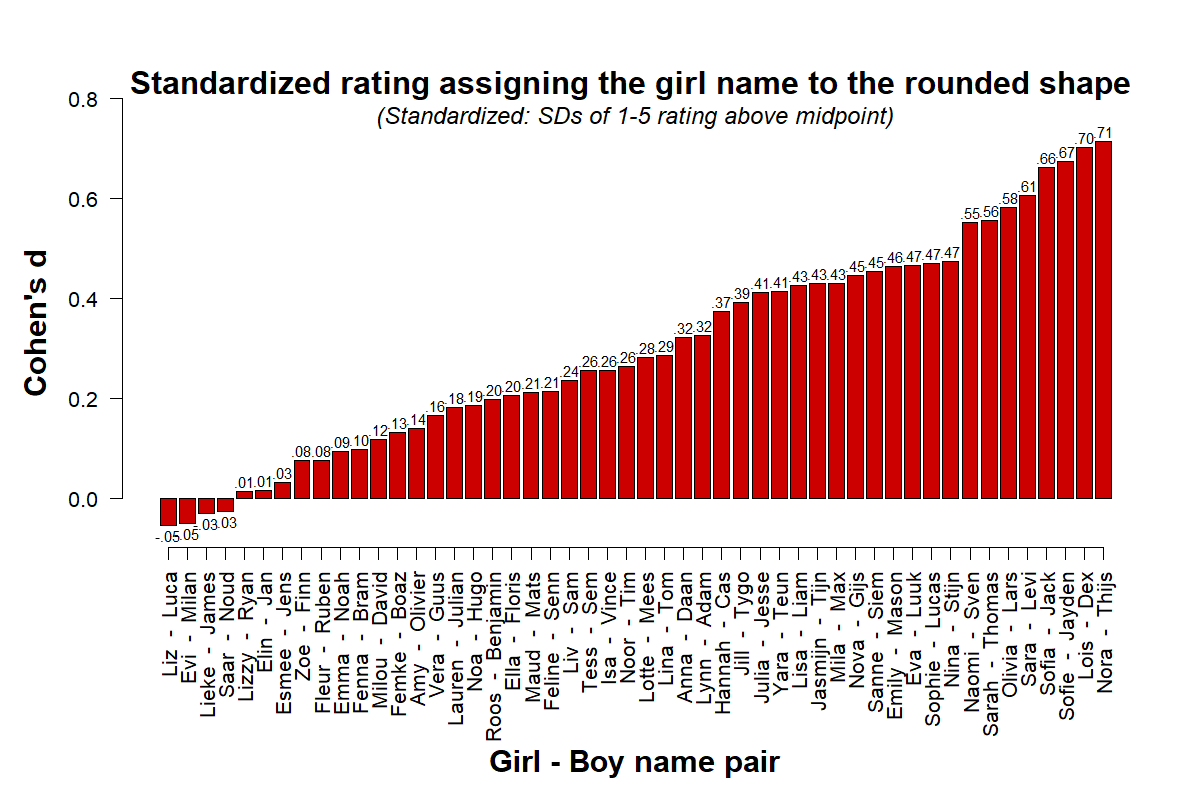
Figure 1. 50 MTurk studies run in June 2017 (N=508). Each participant rated a random subset of 10 name-pairs,
indicating, on a 1-5 scale, the extent to which one name or the other seemed more likely to be the name of the rounded shape (R Code).
For example, the right-most bar shows that Nora (vs. Thijs) was much more likely to be assigned to the round shape (d = 0.71), while the left-most bar shows a slight reversal for Liz (vs. Luca) (d = -0.05).
Running a meta-analysis on these 50 studies, we find that the standard measure of heterogeneity, I2, was quite high, at I2 = 78%, p < .0001 [5]. As a benchmark, consider that Stanley et al., quoted in the intro, computed an average I2=74% across 200 meta-analysis in psychology and wrote that such high heterogeneity makes it "unlikely that any replication will be successful" (p. 1339).
To see whether such extreme pessimism is warranted, we ran all 50 studies again in our Wave 2, about three weeks ago (April 2019), nearly 2 years after Wave 1. The results replicated about as well as can be rationally expected. That is, they varied only as much as would be expected because of sampling error (see Figure 2). For example, if there were zero unobservable heterogeneity, we would expect effect sizes to be correlated r = .79 across waves. Our observed correlation was rather close to that, r = .77 (see footnote for calculations: [6]).
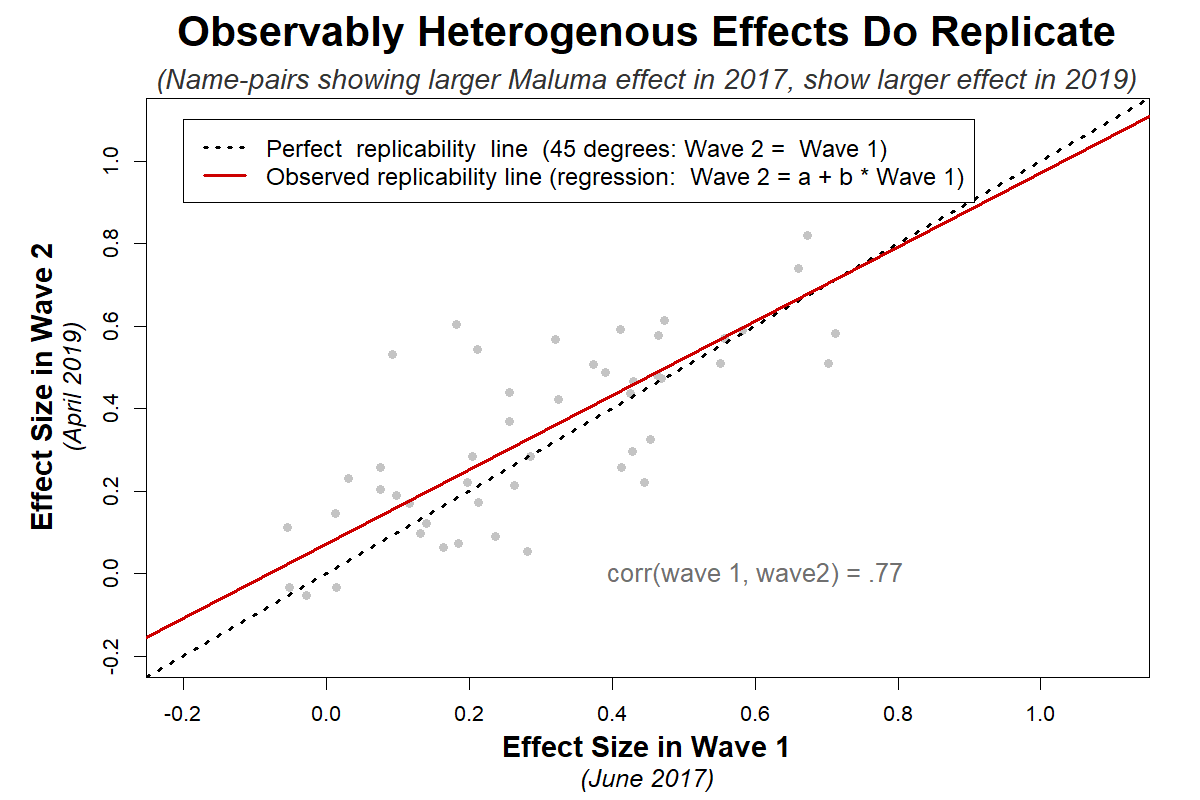
Figure 2. Scatterplot of effect size estimates for 50 name-pairs shown in Figure 1, for two separate MTurk waves (R Code).
When we asked them for feedback on this post, some of the authors we quoted did not think the scatterplot above looks so great for replicability, as there is quite a bit of noise between two estimates of the same study. We are not disputing the reality of sampling error, and it is a fact that studies with just n=100 are noisy. The question is whether they are noisier than expected by chance alone. The answer is 'no.' Perhaps this is easier to appreciate in Figure 3:
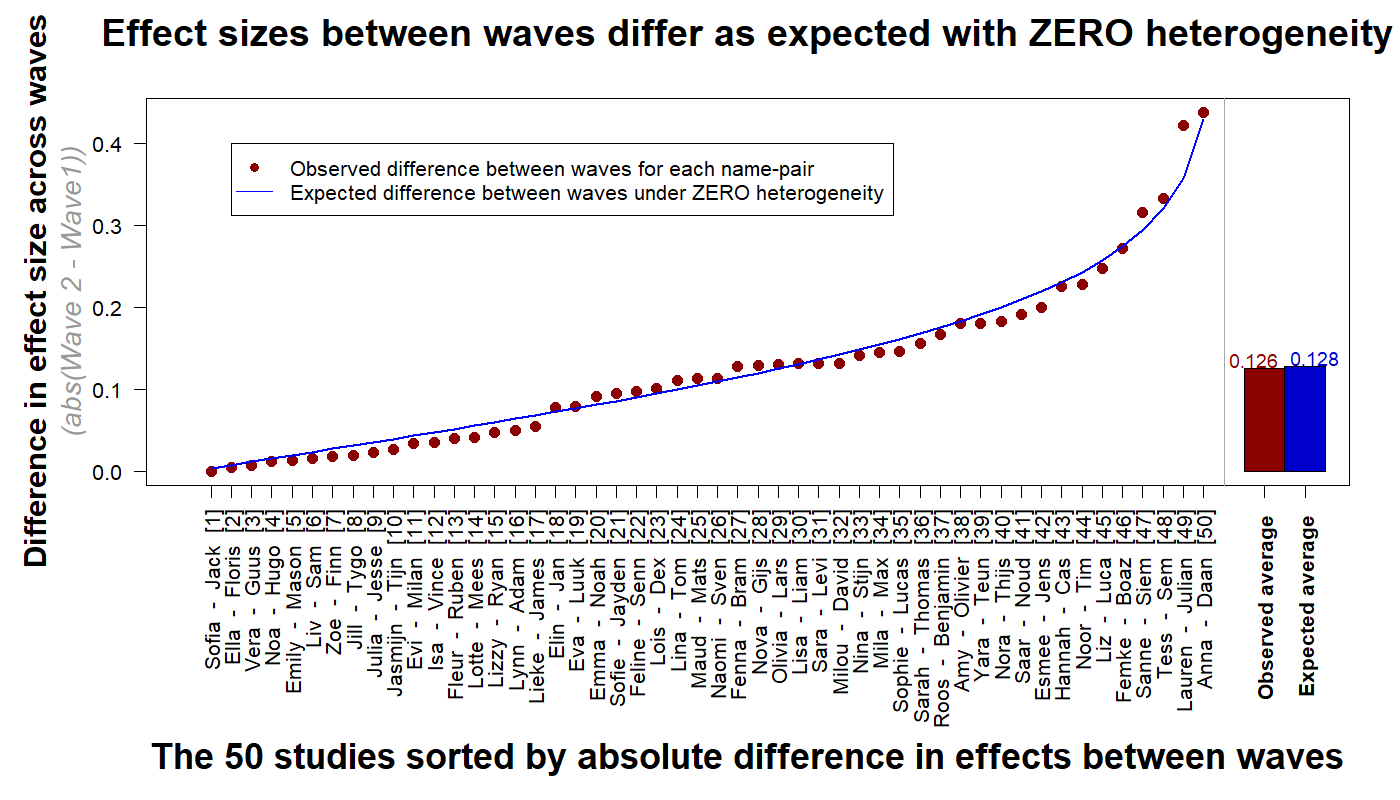
Figure 3. For each of the 50 studies we computed the absolute difference in effect size between waves. The expected (blue) line depicts the average differences in bootstrapped samples when forcing homogeneity, ranked from smallest to largest expected difference. There is zero evidence of unobserved heterogeneity in the MTurk data (R Code)
These results show that while effect sizes were observably quite heterogeneous, unobservable heterogeneity was between nil and trivial, so properly powered replications of these designs would generally be expected to replicate.
These results also show that MTurk is a reliable source of data, providing similar results when the same studies are collected 2 years apart.
Note from 2019 04 25: After receiving an email inquiry, we have re-run all analyses dropping participants who partook in both waves, results are unchanged see footnote for details [7].
Are identical studies really heterogeneous?
Though we found that our 50 MTurk studies conducted two years apart were as stable as one should rationally expect, McShane and colleagues reported high instability in the MTurk results of a Many Labs paper run just days apart.
For example, they wrote:
“treating each [MTurk] day as a separate study […] yields seven extremely close replications […] Again, however, […] heterogeneity is nontrivial: […] nonzero estimates of heterogeneity for nine of the 14 non-null phenomena and across these, [I2= 21%]"
McShane, Böckenholt, and Hansen (2016); .htm
Now, we understand that an I2 of 21% might seem “nontrivial,” or even high, but it is important to keep in mind that even if there were zero unobservable heterogeneity in MTurk across days, we would expect I2 to be greater than zero. There are two reasons for this. First, I2 is, well, a squared value, and squared values can’t be negative. Thus, it is possible for I2 to be greater than zero just by chance, but it can never be less than zero just by chance. Thus, on average, in the presence of zero heterogeneity, we would expect I2 to be greater than zero [8]. Second, I2 is easily biased upwards when you violate its distributional assumptions, and we have shown that this bias is present for the specific data analyzed by McShane et al. (https://datacolada.org/63).
To take both issues into account, we bootstrapped the I2 in the Many Labs data, in order to ascertain what the I2 should be if there were truly no heterogeneity across studies. It turns out we should expect an average I2 of 24%. Recall that we observe slightly less variation than that: I2=21%. The null of homogeneity is not rejected: p = .44 (R Code). The observed amount of heterogeneity is trivial after all.
The Many Labs MTurk data, then, is consistent with our Maluma-Takiti demonstration, and provides no evidence for the presence of hidden moderators.
Many Labs Beyond MTurk
The papers we quoted at the beginning of this post cite a few other Many Labs papers to support the notion that unobserved heterogeneity is a big problem in psychology. For example, McShane et al. mention that the many labs papers by (i) Eerland et al. 2016 and (ii) Hagger et al. (2016) show “moderate amounts of heterogeneity” (p. 101). Kenny and Judd (2018) mention those same two Many Labs papers as evidence of heterogeneity as well. Let’s look at them.
- Eerland et al. (.htm) analyzed three dependent variables. The first shows a high I2 but the null of zero heterogeneity is not terribly inconsistent with the data (p=.045). The other two DVs in that paper show zero heterogeneity (I2 = 0%, with p=.393 and p=.662).
- Hagger et al. (.htm) used two dependent variables. The p-values for heterogeneity were p=.045 and p=.056.
Thus, the five p-values supporting “moderate amounts of heterogeneity” are .045, .045, .056, .662, and .393. We think most impartial observers would agree that this is not strong evidence.
Importantly, there are at least six other Many Labs papers whose heterogeneity results are not mentioned in the context of these arguments. None of them exhibit significant heterogeneity (links to all papers in table: .pdf).
Note: While writing this post we found a coding error in the heterogeneity calculations in Many Labs 3 (Ebersole et al 2016). See footnote for details: [9].
Conclusions
The evidence does not support the general claim that unobservable heterogeneity is inevitable in psychology, nor the specific claim that identical designs across different labs, or across time on MTurk, obtain surprisingly heterogeneous results.
One theme in the original papers we quoted from is that heterogeneity makes it challenging to generalize effect size estimates from one design to another design. We fully agree with this. Moreover, we agree with Judd and Kenny that it is valuable to engage in "stimulus sampling," to include variations of stimuli within individual experiments. (If you are unfamiliar with stimulus sampling, please check out this important paper: .htm).
But generalizability and replicability are different concepts. To establish that a finding is a scientific fact, you need to establish that it replicates under some specifiable condition(s). But you do not need to establish that it generalizes. For example, if I claim to have shown that people can levitate when they drink vanilla lattes, then I need to show that they can levitate under some set of predictable and reproducible conditions (i.e., when they drink vanilla lattes), but I do not need to show that they can levitate under other conditions (e.g., when they drink cappuccinos). Of course, whether they can also levitate when they drink cappuccinos is an interesting and important question, one that has implications for our understanding of why and how levitation might occur. But it makes no sense to ask whether my levitation finding is generalizable if I cannot first establish that it is replicable. Replicability is always the first thing that needs to be established, because without it there is no finding to explain or understand (see Colada[53]). We believe that these authors have conflated replicability and generalizability, and that that conflation lies at the root of our disagreement with them.
The question of interest in this post is whether, in the presence of observable heterogeneity across different experimental designs, single-study direct replications can be informative if they are properly powered. For example, can we ex ante predict that people will assign Nora to the rounded shape more often than Thijs? Can we ex ante predict that the Nora-Thijs difference will be greater than the Liz-Luca difference?
Our read of the quoted papers is that they say "no."
Our read of the evidence is that it says "yes."
![]()
Author feedback
Our policy (.htm) is to share drafts of blog posts that discuss someone else’s work with them to solicit suggestions for things we should change prior to posting. We contacted all authors of the original quoted in the introduction, and the first author of Many Labs 3. We heard back from all teams. In response to their feedback, we corrected a few errors (specifically to some of the I2 p-values we were copy-pasting), added a bootstrap analysis of Maluma that draws participants rather than single ratings at random, added Figure 3, and made a few other clarifications throughout. We also revised the writing in an attempt to clarify the overall message of each of their papers, and why we ran the analyses that we did. We thank all of them for responding to our request for feedback.
After a few email exchanges with Chick Judd and Dave Kenny, we identified the following issue that's at the heart of our disagreement. As they put it in an email to us "For us (Judd & Kenny), inevitably any attempt at replication involves generalization because the exact same situation, samples, and so on cannot be recreated. Some of these changes likely moderate the effect, and even possibly there might be fundamentally random variation in the effect. The result is heterogeneity, even in ‘exact’ replications. We agree that the evidence for heterogeneity is weak in the case of null or essentially zero effects. The evidence is considerably stronger for non-null effects.” We (Joe and Uri) disagree with them because to us the evidence available so far suggests the consequences of such minimal levels of unobservable heterogeneity are basically nil, thus 'exact' replications are often, in practice, obtained (e.g., our Maluma demonstration). All 4 of us agreed to include this summary.
Footnotes.
- When writing this post we learned, with some consternation, that Köhler, in his original study, spelled Takiti as “Takete”. For a German in the late 1920s, we code this as a minor transgression. Actually, writing this footnote led us to look up Wolfgang Köhler (.htm). He was a vocal opponent of the Nazi regime and emigrated to our beloved Pennsylvania in the 1930s. He was a Swarthmore professor until 1955. [↩]
- Although Köhler gets the credit for this work, we have to give a shout out to Yale’s Shane Frederick for popularizing it in the JDM community. He is the reason we know about this. [↩]
- We counterbalanced the order of boy vs. girl names across the 50 studies [↩]
- The Many Labs papers, currently used as the best estimates of unobservable heterogeneity in psychology, also had participants complete multiple studies. [↩]
- This means that 78% of the variance across studies is beyond what's expected by chance. I2 is a bad measure of heterogeneity (see Colada[63]), but we use it anyway because the authors whose work we are commenting on used it [↩]
- To create the expected correlation between studies in the absence of heterogeneity, we shuffled observations between Waves 1 and 2 within each study, 10,000 times. This forces the null of no heterogeneity on the data, while preserving most other relevant data structures. The average correlation of these reshuffled datasets was r = .789. The figure below contrasts the observed with the expected correlation under the null.
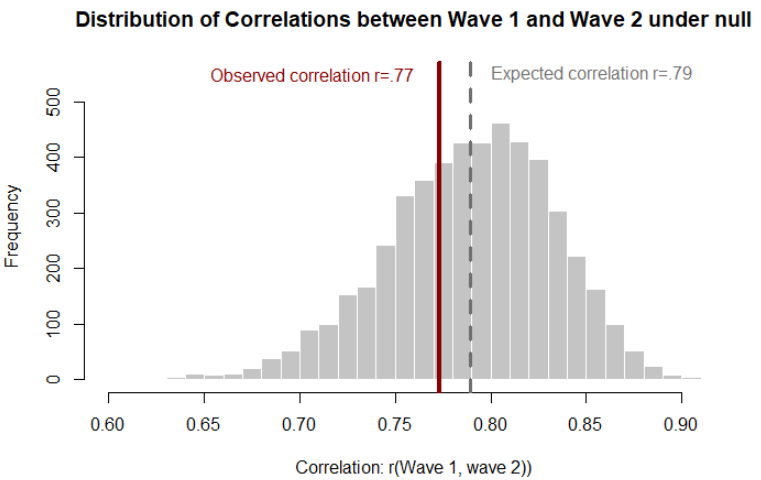
Figure A1. Distribution of correlations between two waves of the same 50 studies under the null that there is zero unobserved heterogeneity within study design across time. The observed correlation, r=.77, is close to the center of the distribution expected under the null.If the bootstrap is done by drawing only from Wave 1 to create Waves 1 and 2, the expected correlation is similar: r=.786.
If the bootstrap is done by drawing participants at random, so all the ratings of a given participant bundled for any given draw, taking into account the lack of independence across observations by the same participant, the expected correlation is unchanged: r=.795. See R Code Section #3.8 [↩] - There are 36 MTurk IDs that appear on both waves, these are probably repeat participants. If we drop them (from both waves) the results are as follows. I2 in wave 1 goes from 78.4% to 76.7%. Correlation of Wave 1 and Wave 2 effects goes from r=.773 to r=.790 [↩]
- It is possible to obtain I2=0, but the probability of obtaining I2>0 when they is zero heterogeneity is typically greater than 0.40. See R Code. [↩]
- There are two significant results among the 13 they report, but that's due to a coding error, where the signs of a few estimates were mistakenly reversed, thus artificially inflating the estimates of heterogeneity. The authors are working on a correction. In our Table 1, we report the the results as published (p = .17). The correct p-value is substantially higher than p =. 17. [↩]