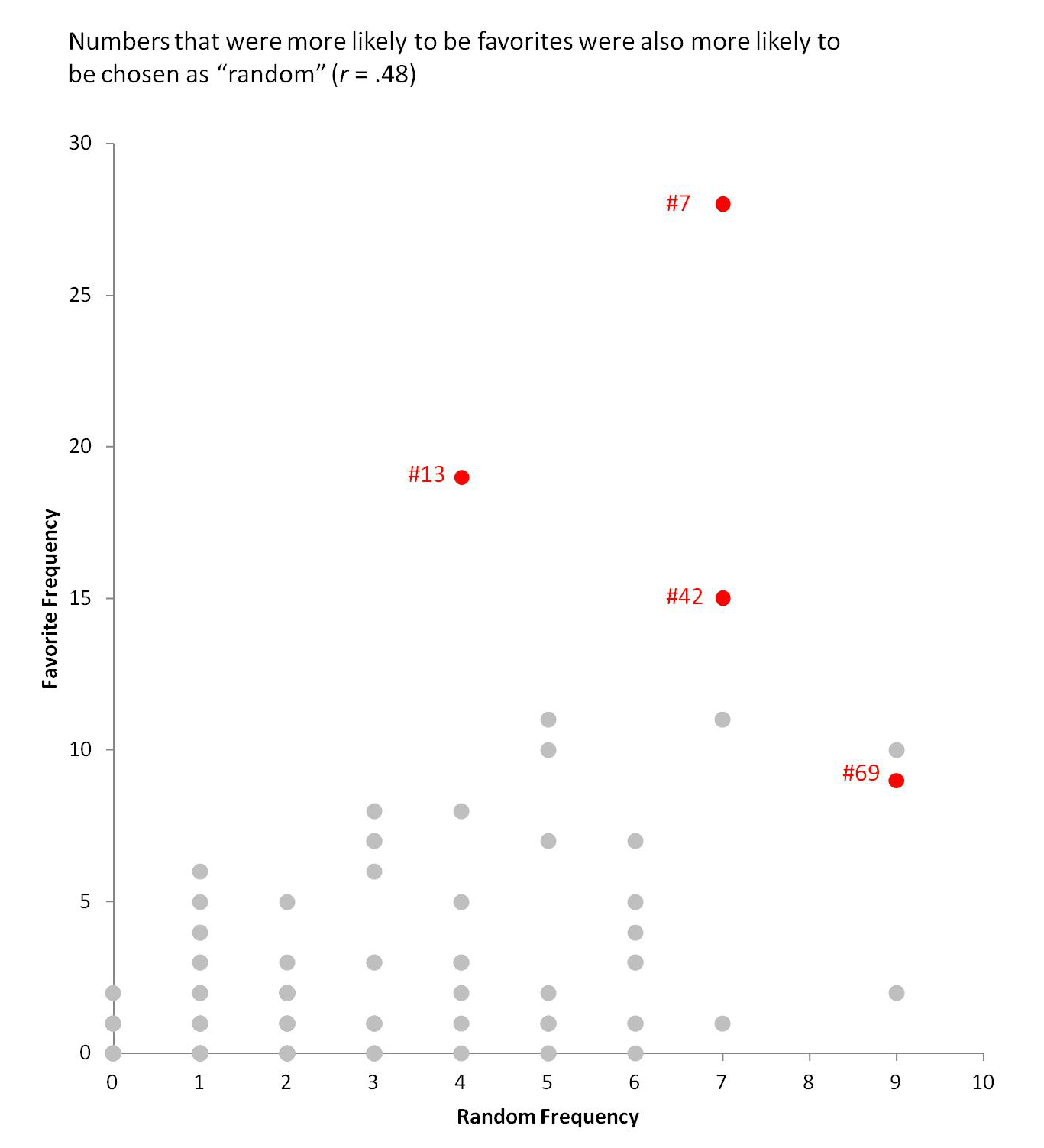
What’s your favorite number between 1 and 100? Now, think of a random number between 1 and 100. My goal for this post is to compare those two responses.
Number preferences feel random. They aren’t. “Random” numbers also feel random. Those aren’t random either. I collected some data, found a pair of austere academic papers, and one outstanding blog post. I will tell you about all of them.
First, the data I collected. I (along with Hannah Perfecto, one of my excellent doctoral students) asked one group of people to generate a random number between 1 and 100. Another group reported their favorite number between 1 and 100. That’s it.
We know a little about preferences. People like their birthday numbers, for example. They pursue round numbers. In preparing this post, I learned of a simmering literature on single-digit number preferences, suggesting that in both 1971 and in 1988 people liked the number 7. (Aside: Someone should write the number preference equivalent of the Princeton Trilogy. In fact, why not move beyond preferences to other attributes? For example, are even numbers more warm or more competent?*). As far as I can tell, less is known about how people generate random numbers. Do people choose the same numbers at random as they choose as their favorites?
The figures tell the whole story, but words are useful. Consider four notable numbers. Consistent with past research, people like the number 7. Inconsistent with horror movie titlers and hotel floor number assigners, people also like the number 13. The number 42 has an entirely wonderful Wikipedia entry, suggesting that its consequence goes beyond Jackie Robinson and Douglas Adams. Perhaps the Data Colada can add a small footnote to its mystique? Finally, the number 69 also has a Wikipedia entry, though it is far less vivid than you’re anticipating. On the random side there are fewer obvious winners (three way tie between 5, 67, and 69). 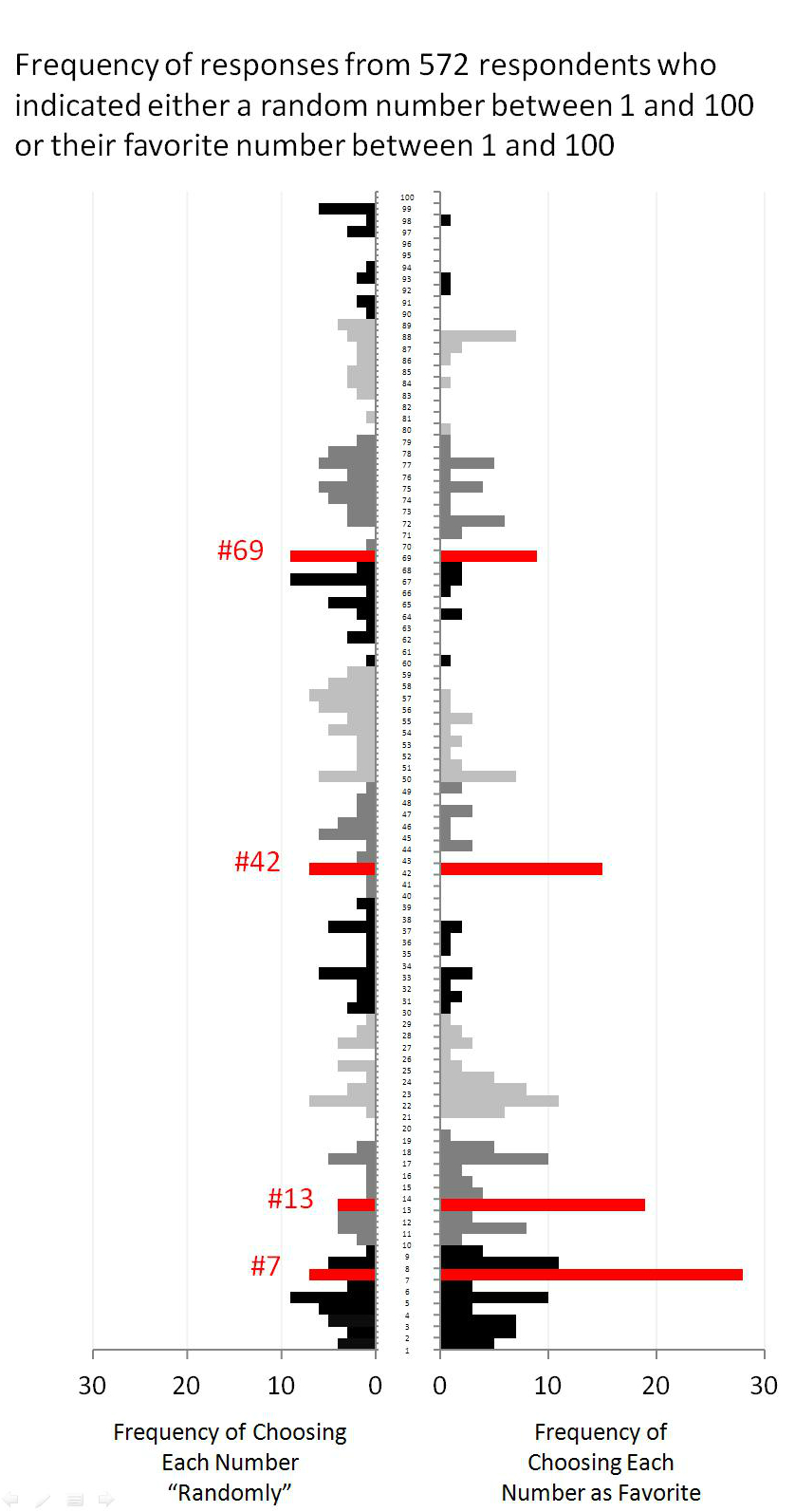
How about some other patterns? First of all, the two sets are highly, but imperfectly, correlated at r = .48. Random numbers are larger than favorite numbers (Ms = 46.9 vs. 30.7), t(565) = 7.01, p
These tendencies are partially reflected in the numeric codes people choose for debit cards and their ilk. PIN numbers are a mix of preference and random, and consistent with the data we collected, a brilliant analysis of leaked PIN numbers reveals birthday liking (numbers below 32) and repeated numbers (like multiples of 11). Figure 3 reproduces a chart of 4-digit PIN codes. It will take 30 seconds to orient yourself, but then you will spend five minutes savoring it. 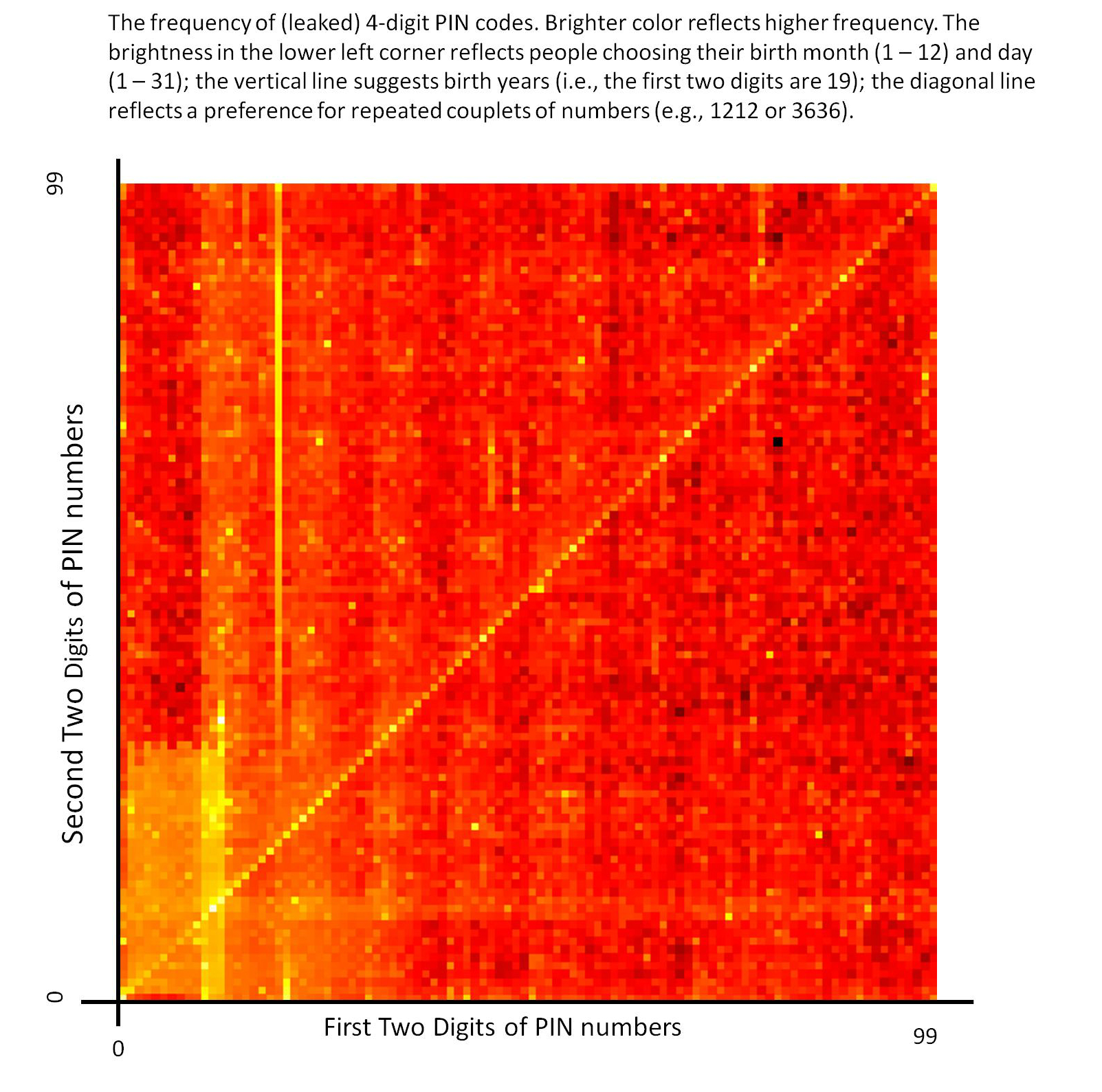
My favorite number is just about the most arbitrary preference possible. My “random” number is more arbitrary. But neither is arbitrary at all.
* Hypothesis: More warm. Odd numbers are wicked competent.