Many believe that while p-hacking invalidates p-values, it does not invalidate Bayesian inference. Many are wrong.
This blog post presents two examples from my new “Posterior-Hacking” (SSRN) paper showing selective reporting invalidates Bayesian inference as much as it invalidates p-values.
Example 1. Chronological Rejuvenation experiment
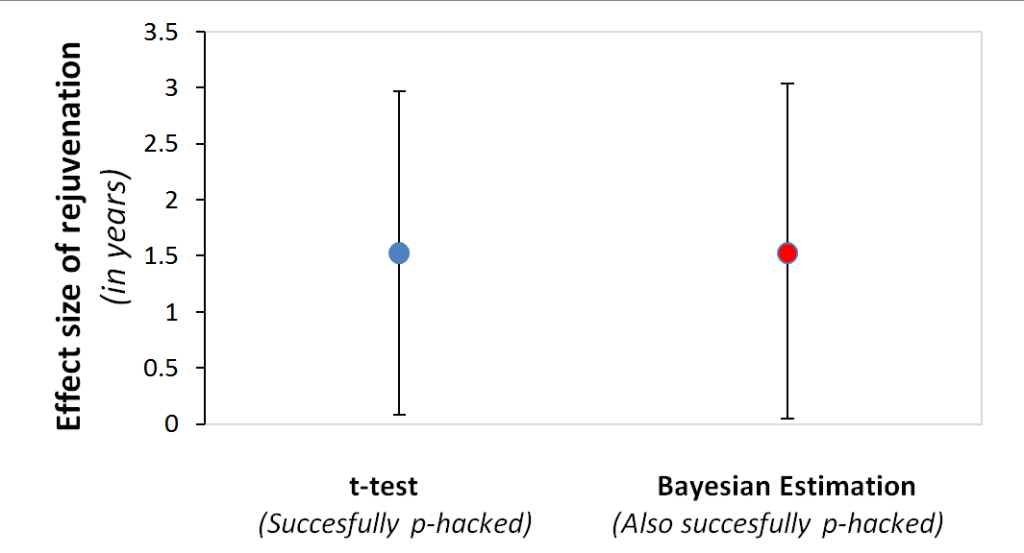
In “False-Positive Psychology" (SSRN), Joe, Leif and I run experiments to demonstrate how easy p-hacking makes it to obtain statistically significant evidence for any effect, no matter how untrue. In Study 2 we “showed” that undergraduates randomly assigned to listen to the song “When I am 64” became 1.4 years younger (p<.05).
We obtained this absurd result by data-peeking, dropping a condition, and cherry-picking a covariate. p-hacking allowed us to fool Mr. p-value. Would it fool Mrs. Posterior also? If we take the selectively reported result and feed it to a Bayesian calculator. What happens?
The figure below shows traditional and Bayesian 95% confidence intervals for the above mentioned 1.4 years-younger chronological rejuvenation effect. Both point just as strongly (or weakly) toward the absurd effect existing. [1]
When researchers p-hack they also posterior-hack
Example 2. Simulating p-hacks
Many Bayesian advocates propose concluding an experiment suggests an effect exists if the data are at least three times more likely under the alternative than under the null hypothesis. This “Bayes factor>3” approach is philosophically different, and mathematically more complex than computing p-values, but it is in practice extremely similar to simply requiring p< .01 for statistical significance. I hence run simulations assessing how p-hacking facilitates getting p<.01 vs getting Bayes factor>3. [2]
I simulated difference-of-means t-tests p-hacked via data-peeking (getting n=20 per-cell, going to n=30 if necessary), cherry-picking among three dependent variables, dropping a condition, and dropping outliers. See R-code.
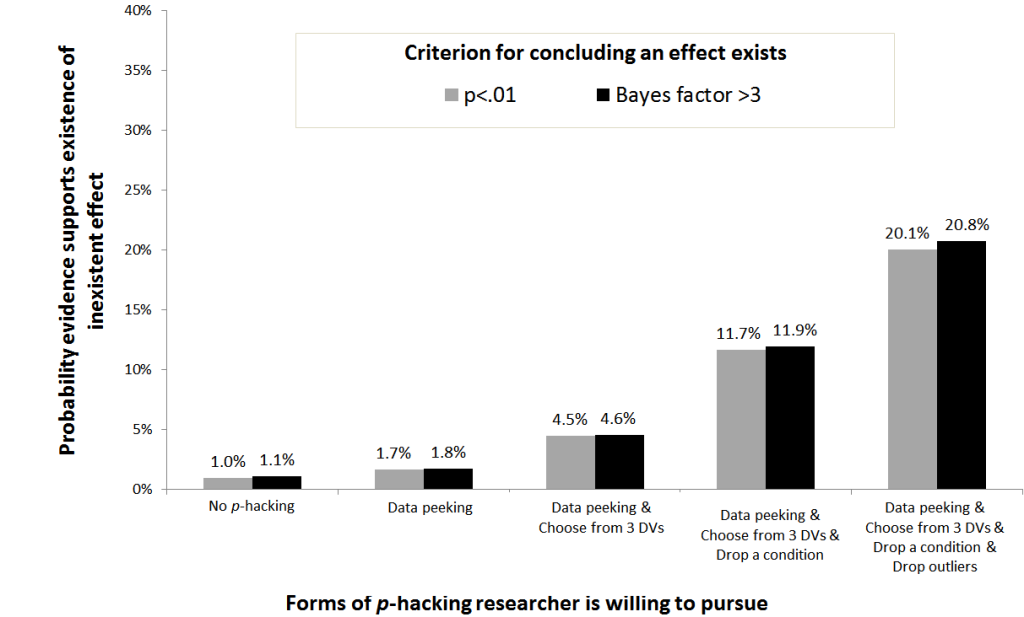
Adding 10 observations to samples of size n=20 a researcher can increase her false-positive rate from the nominal 1% to 1.7%. The probability of getting a Bayes factor >3 is a comparable 1.8%. Combined with other forms of p-hacking, the ease with which a false finding is obtained increases multiplicatively. A researcher willing to engage in any of the four forms of p-hacking, has a 20.1% chance of obtaining p<.01, and a 20.8% chance of obtaining a Bayes factor >3.
When a researcher p-hacks, she also Bayes-factor-hacks.
Everyone needs disclosure
Andrew Gelman and colleagues, in their influential Bayesian textbook write:
A naïve student of Bayesian inference might claim that because all inference is conditional on the observed data, it makes no difference how those data were collected, […] the essential flaw in the argument is that a complete definition of ‘the observed data’ should include information on how the observed values arose […]”
(p.203, 2nd edition)
Whether doing traditional or Bayesian statistics, without disclosure, we cannot evaluate evidence.
- The Bayesian confidence interval is the “highest density posterior interval”, computed using Kruschke's BMLR (html). [↩]
- This equivalence is for the default-alternative, see Table 1 in Rouder et al, 2009 (HTML). [↩]