Some journals are thinking of discouraging authors from reporting p-values and encouraging or even requiring them to report confidence intervals instead. Would our inferences be better, or even just different, if we reported confidence intervals instead of p-values?
One possibility is that researchers become less obsessed with the arbitrary significant/not-significant dichotomy. We start paying more attention to effect size. We start paying attention to precision. A step in the right direction.
Another possibility is that researchers forced to report confidence intervals will use them as if they were p-values and will only ask “Does the confidence interval include 0?” In this world confidence intervals are worse than p-values, because p=.012, p=.0002, p=.049 all become p<.05. Our analyses become more dichotomous. A step in the wrong direction.
How to test this?
To empirically assess the consequences of forcing researchers to replace p-values with confidence intervals we could randomly impose the requirement on some authors and see what happens.
That's hard to pull off for a blog post. Instead, I exploit a quirk in how "mediation analysis" is now reported in psychology. In particular, the statistical program everyone uses to run mediation reports confidence intervals rather than p-values. How are researchers analyzing those confidence intervals?
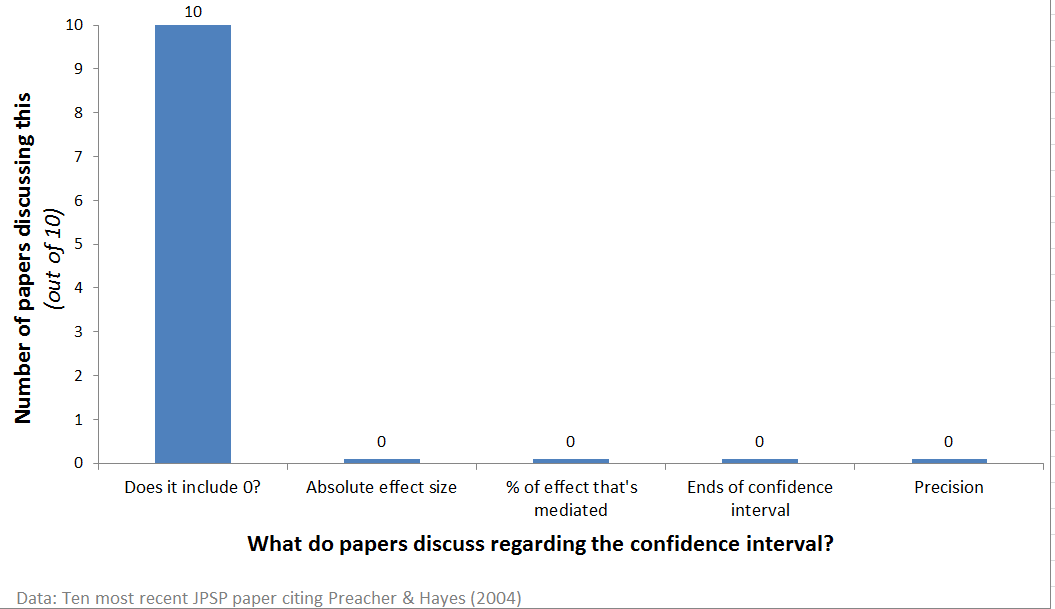
Sample: 10 papers
I went to Web-of-Science and found the ten most recent JPSP articles (.html) citing the Preacher and Hayes (2004) article that provided the statistical programs that everyone runs (.pdf).
All ten of them used confidence intervals as dichotomus p-values, none discussed effect size or precision. None discussed the percentage of the effect that was mediated. One even accepted the null of no mediation because the confidence interval included 0 (it also included large effects).
This sample suggests confidence intervals do not change how we think of data.
If people don’t care about effect size here…
Unlike other effect-size estimates in the lab, effect-size in mediation is intrinsically valuable.
No one asks how much more hot sauce subjects pour for a confederate to consume after watching a film that made them angry, but we do ask how much of that effect is mediated by anger; ideally all of it. [1]
Change the question before you change the answer
If we want researchers to care about effect size and precision, then we have to persuade researchers that effect size and precision are important.
I have not been persuaded yet. Effect size matters outside the lab for sure. But in the lab not so clear. Our theories don't make quantitative predictions, effect sizes in the lab are not particularly indicative of how important a phenomenon is outside the lab, and to study effect size with even moderate precision we need samples too big to plausibly be run in the lab (see Colada[20]). [2]
My talk at a recent conference (SESP) focused on how research questions should shape the statistical tools we choose to run and report. Here are the slides (.pptx). This post is an extension of Slide #21.
![]()
- In practice we do not measure things perfectly, so going for 100% mediation is too ambitious [↩]
- I do not have anything against reporting confidence intervals alongside p-values. They will probably be ignored by most readers, but a few will be happy to see them, and it is generally good to make people happy (Though it is worth pointing out that one can usually easily compute confidence intervals from test results). Descriptive statistics more generally, e.g., means and SDs, should always be reported to catch errors, facilitate meta-analyses, and just generally better understand the results. [↩]