When considering any statistical tool I think it is useful to answer the following two practical questions:
1. “Does it give reasonable answers in realistic circumstances?”
2. “Does it answer a question I am interested in?”
In this post I explain why, for me, when it comes to the default Bayesian test that's starting to pop up in some psychology publications, the answer to both questions is “no.”
The Bayesian test
The Bayesian approach to testing hypotheses is neat and compelling. In principle. [1]
The p-value assesses only how incompatible the data are with the null hypothesis. The Bayesian approach, in contrast, assesses the relative compatibility of the data with a null vs an alternative hypothesis.
The devil is in choosing that alternative. If the effect is not zero, what is it?
Bayesian advocates in psychology have proposed using a “default” alternative (Rouder et al 1999, .pdf). This default is used in the online (.html) and R based (.html) Bayes factor calculators. The original papers do warn attentive readers that the default can be replaced with alternatives informed by expertise or beliefs (see especially Dienes 2011 .pdf), but most researchers leave the default unchanged. [2]
This post is written with that majority of default following researchers in mind. I explain why, for me, when running the default Bayesian test, the answer to Questions 1 & 2 is "no" .
Question 1. “Does it give reasonable answers in realistic circumstances?”
No. It is prejudiced against small effects
The null hypothesis is that the effect size (henceforth d) is zero. Ho: d = 0. What's the alternative hypothesis? It can be whatever we want it to be, say, Ha: d = .5. We would then ask: are the data more compatible with d = 0 or are they more compatible with d = .5?
The default alternative hypothesis used in the Bayesian test is a bit more complicated. It is a distribution, so more like Ha: d~N(0,1). So we ask if the data are more compatible with zero or with d~N(0,1). [3]
That the alternative is a distribution makes it difficult to think about the test intuitively. Let's not worry about that. The key thing for us is that that default is prejudiced against small effects.
Intuitively (but not literally), that default means the Bayesian test ends up asking: “is the effect zero, or is it biggish?” When the effect is neither, when it’s small, the Bayesian test ends up concluding (erroneously) it's zero. [4]
Demo 1. Power at 50%
Let's see how the test behaves as the effect size get smaller (R Code)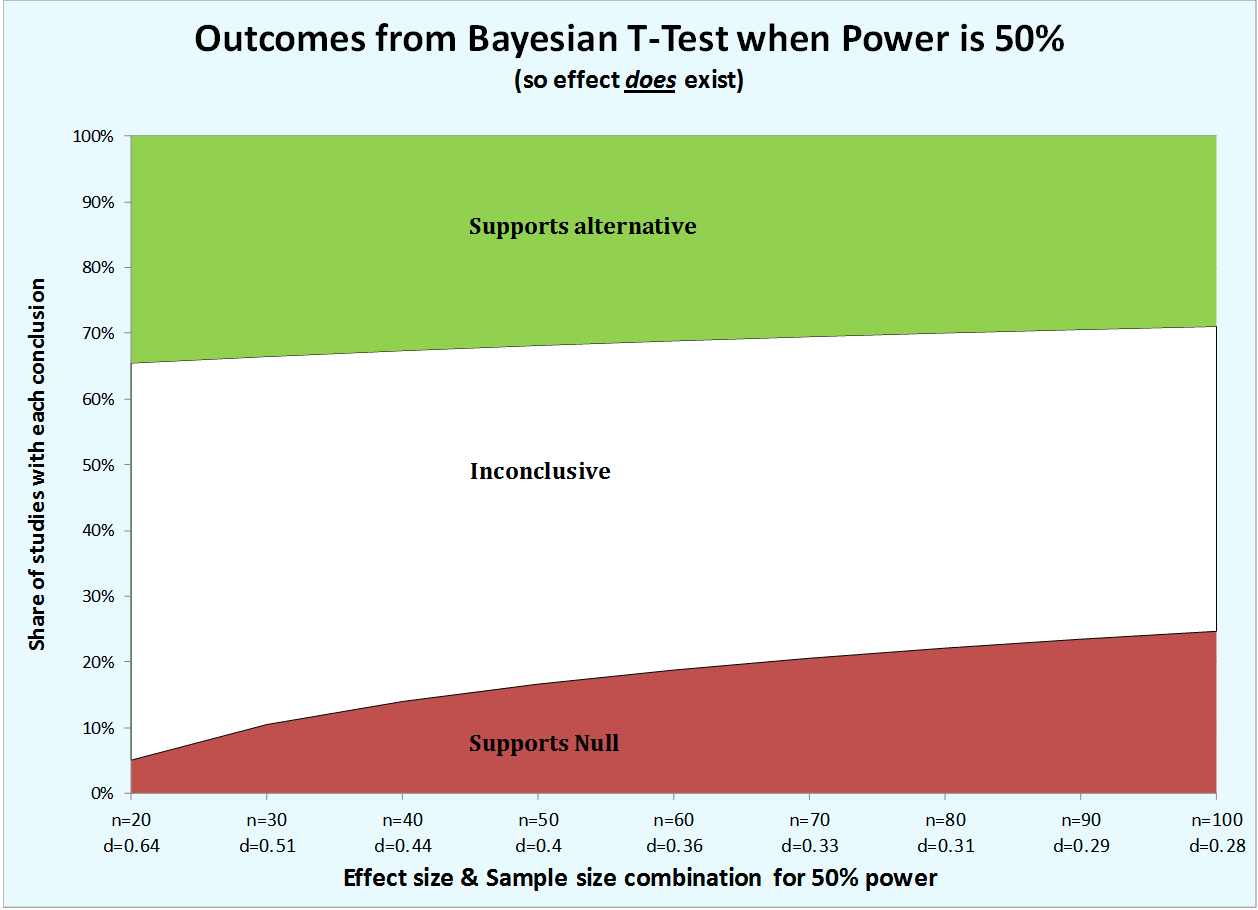 The Bayesian test erroneously supports the null about 5% of the time when the effect is biggish, d=.64, but it does so five times more frequently when it is smallish, d=.28. The smaller the effect (for studies with a given level of power), the more likely we are to dismiss its existence. We are prejudiced against small effects. [5]
The Bayesian test erroneously supports the null about 5% of the time when the effect is biggish, d=.64, but it does so five times more frequently when it is smallish, d=.28. The smaller the effect (for studies with a given level of power), the more likely we are to dismiss its existence. We are prejudiced against small effects. [5]
Note how as sample gets larger the test becomes more confident (smaller white area) and more wrong (larger red area).
Demo 2. Facebook
For a more tangible example consider the Facebook experiment (.html) that found that seeing images of friends who voted (see panel a below) increased voting by 0.39% (panel b). While the null of a zero effect is rejected (p=.02) and hence the entire confidence interval for the effect is above zero, [6] the Bayesian test concludes VERY strongly in favor of the null, 35:1. (R Code)
While the null of a zero effect is rejected (p=.02) and hence the entire confidence interval for the effect is above zero, [6] the Bayesian test concludes VERY strongly in favor of the null, 35:1. (R Code)
Prejudiced against (in this case very) small effects.
Question 2. “Does it answer a question I am interested in?”
No. I am not interested in how well data support one elegant distribution.
When people run a Bayesian test they like writing things like
"The data support the null."
But that’s not quite right. What they actually ought to write is
"The data support the null more than they support one mathematically elegant alternative hypothesis I compared it to"
Saying a Bayesian test “supports the null” in absolute terms seems as fallacious to me as interpreting the p-value as the probability that the null is false.
We are constantly reminded that:
P(D|H0)≠P(H0)
The probability of the data given the null is not the probability of the null
But let’s not forget that:
P(H0|D) / P(H1|D) ≠ P(H0)
The relative probability of the null over one mathematically elegant alternative is not the probability of the null either.
Because I am not interested in the distribution designated as the alternative hypothesis, I am not interested in how well the data support it. The default Bayesian test does not answer a question I would ask.
![]()
Feedback from Bayesian advocates:
I shared an early draft of this post with three Bayesian advocates. I asked for feedback and invited them to comment.
1. Andrew Gelman Expressed "100% agreement" with my argument but thought I should make it clearer this is not the only Bayesian approach, e.g., he writes "You can spend your entire life doing Bayesian inference without ever computing these Bayesian Factors." I made several edits in response to his suggestions, including changing the title.
2. Jeff Rouder Provided additional feedback and also wrote a formal reply (.html). He begins highlighting the importance of comparing p-values and Bayesian Factors when -as is the case in reality- we don't know if the effect does or does not exist, and the paramount importance for science of subjecting specific predictions to data analysis (again, full reply: .html)
3. EJ Wagenmakers Provided feedback on terminology, the poetic response that follows, and a more in-depth critique of confidence intervals (.pdf)
In a desert of incoherent frequentist testing there blooms a Bayesian flower. You may not think it is a perfect flower. Its color may not appeal to you, and it may even have a thorn. But it is a flower, in the middle of a desert. Instead of critiquing the color of the flower, or the prickliness of its thorn, you might consider planting your own flower — with a different color, and perhaps without the thorn. Then everybody can benefit.”
Footnotes.
- If you want to learn more about it I recommend Rouder et al. 1999 (.pdf), Wagenmakers 2007 (.pdf) and Dienes 2011 (.pdf) [↩]
- e.g., Rouder et al (.pdf) write “We recommend that researchers incorporate information when they believe it to be appropriate […] Researchers may also incorporate expectations and goals for specific experimental contexts by tuning the scale of the prior on effect size” p.232 [↩]
- The current default distribution is d~N(0,.707), the simulations in this post use that default [↩]
- Again, Bayesian advocates are upfront about this, but one has to read their technical papers attentively. Here is an example in Rouder et al (.pdf) page 30: “it is helpful to recall that the marginal likelihood of a composite hypothesis is the weighted average of the likelihood over all constituent point hypotheses, where the prior serves as the weight. As [variance of the alternative hypothesis] is increased, there is greater relative weight on larger values of [the effect size] […] When these unreasonably large values […] have increasing weight, the average favors the null to a greater extent”. [↩]
- The convention is to say that the evidence clearly supports the null if the data are at least three times more likely when the null hypothesis is true than when the alternative hypothesis is, and vice versa. In the chart above I refer to data that do not clearly support the null nor the alternative as inconclusive. [↩]
- note that the figure plots standard errors, not a confidence interval [↩]

